题目内容
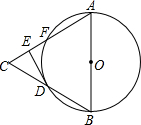 如图,在等边三角形△ABC中,以AB为直径的⊙O交BC于点D,交AC于点F,过D作⊙O的切线交AC于E.若DE=2,则⊙O的面积等于
如图,在等边三角形△ABC中,以AB为直径的⊙O交BC于点D,交AC于点F,过D作⊙O的切线交AC于E.若DE=2,则⊙O的面积等于考点:切线的性质
专题:
分析:连接OD,易证得△OBD是等边三角形,得出∠C=∠ODB,证得OD∥AC,进而证得CD=DB,根据切线的性质证得∠ODE=90°,即可证得∠EDC=30°,从而证得△CDE是直角三角形,通过解直角三角形求得CD,即可求得圆的半径,根据圆的面积公式即可求得.
解答:
 解:连接OD,
解:连接OD,
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∴OD=OB,
∴△OBD是等边三角形,
∴∠ODB=60°,
∴∠C=∠ODB,
∴OD∥AC,
∴OA=OB,
∴CD=DB,
∵DE是⊙O的切线,
∴OD⊥DE,
∵∠ODC=120°,
∴∠EDC=30°,
∴∠DEC=180°-∠C-∠EDC=180°-60°-30°=90°,
∴CD=
=
=
,
∴BD=
=OB,
∴S=(
)2π=
π.
故答案为
π.
 解:连接OD,
解:连接OD,∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∴OD=OB,
∴△OBD是等边三角形,
∴∠ODB=60°,
∴∠C=∠ODB,
∴OD∥AC,
∴OA=OB,
∴CD=DB,
∵DE是⊙O的切线,
∴OD⊥DE,
∵∠ODC=120°,
∴∠EDC=30°,
∴∠DEC=180°-∠C-∠EDC=180°-60°-30°=90°,
∴CD=
| DE | ||||
|
| 2 | ||||
|
4
| ||
| 3 |
∴BD=
4
| ||
| 3 |
∴S=(
4
| ||
| 3 |
| 16 |
| 3 |
故答案为
| 16 |
| 3 |
点评:本题考查了等边三角形的判定和性质,切线的性质,平行线的判定和性质,以及解直角三角形等,连接OD得出OD⊥DE是本题的关键.

练习册系列答案
相关题目
大于-3.1且不大于2的整数共有( )
| A、7个 | B、6个 | C、5个 | D、无数个 |
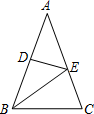 如图,等腰△ABC的周长为16,底边BC=4,AB=AC,∠A=36°,线段AB的垂直平分线交AB于点D,交AC于点E,连接BE.则下列说法中错误的是( )
如图,等腰△ABC的周长为16,底边BC=4,AB=AC,∠A=36°,线段AB的垂直平分线交AB于点D,交AC于点E,连接BE.则下列说法中错误的是( )| A、△CBE是等腰三角形 |
| B、BE平分∠ABC |
| C、△ABE的周长为12 |
| D、△CBE的周长为10 |
若x2+2(m-3)x+16是完全平方式,则m的值等于( )
| A、3 | B、-5 | C、7 | D、7或-1 |

 已知:如图,AD是△ABC的角平分线,过D点分别作AC和AB的平行线,交AB于点E,交AC于点F.
已知:如图,AD是△ABC的角平分线,过D点分别作AC和AB的平行线,交AB于点E,交AC于点F.