题目内容

9．如图，在正方形ABCD中，等边三角形AEF的顶点E、F分别在边BC和CD上，则∠AEB=75度．

分析 只要证明△ABE≌△ADF，可得∠BAE=∠DAF=（90°-60°）÷2=15°，即可解决问题．

解答 解：∵四边形ABCD是正方形，
∴AB=AD，∠B=∠D=∠BAD=90°，
在Rt△ABE和Rt△ADF中，
$\left\{\begin{array}{l}{AB=AD}\\{AE=AF}\end{array}\right.$，
∴△ABE≌△ADF，
∴∠BAE=∠DAF=（90°-60°）÷2=15°，
∴∠AEB=75°，
故答案为75．

点评 本题考查正方形的性质、等边三角形的性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．

练习册系列答案
相关题目
19．在平面直角坐标系中，我们定义直线y=ax-a为抛物线y=ax2+bx+c（a、b、c为常数，a≠0）的“梦想直线”；有一个顶点在抛物线上，另有一个顶点在y轴上的三角形为其“梦想三角形”．

已知抛物线y=-$\frac{2\sqrt{3}}{3}$x2-$\frac{4\sqrt{3}}{3}$x+2$\sqrt{3}$与其“梦想直线”交于A、B两点（点A在点B的左侧），与x轴负半轴交于点C．
（1）填空：该抛物线的“梦想直线”的解析式为y=-$\frac{2\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$，点A的坐标为（-2，2$\sqrt{3}$），点B的坐标为（1，0）；
（2）如图，点M为线段CB上一动点，将△ACM以AM所在直线为对称轴翻折，点C的对称点为N，若△AMN为该抛物线的“梦想三角形”，求点N的坐标；
（3）当点E在抛物线的对称轴上运动时，在该抛物线的“梦想直线”上，是否存在点F，使得以点A、C、E、F为顶点的四边形为平行四边形？若存在，请直接写出点E、F的坐标；若不存在，请说明理由．
20．如图，由四个正方体组成的几何体的左视图是（　　）
A．B．C．D．
17．为加强中小学生安全教育，某校组织了“防溺水”知识竞赛，对表现优异的班级进行奖励，学校购买了若干副乒乓球拍和羽毛球拍．购买2副乒乓球拍和1副羽毛球拍共需116元；购买3副乒乓球拍和2副羽毛球拍共需204元．
（1）求购买1副乒乓球拍和1副羽毛球拍各需多少元；
（2）若学校购买乒乓球拍和羽毛球拍共30副，且支出不超过1480元，则最多能够购买多少副羽毛球拍？
4．如图，梯形ABCD中，AB∥CD，∠D=（　　）
A．120°B．135°C．145°D．155°
14．如图所示，点P到直线l的距离是（　　）
A．线段PA的长度B．线段PB的长度C．线段PC的长度D．线段PD的长度
1．写出一个比3大且比4小的无理数：π．
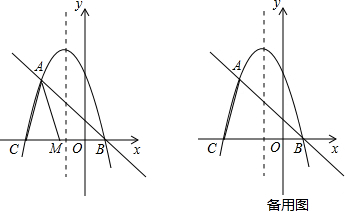
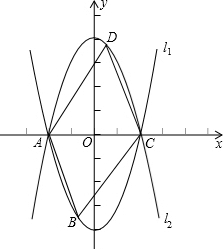7．如图，抛物线l1：y=x2-4的图象与x轴交于A，C两点，抛物线l2与l1关于x轴对称．
（1）直接写出l2所对应的函数表达式；
（2）若点B是抛物线l2上的动点（B与A，C不重合），以AC为对角线，A，B，C三点为顶点的平行四边形的第四个顶点为D，求证：D点在l2上．
（3）当点B位于l1在x轴下方的图象上，平行四边形ABCD的面积是否存在最大值和最小值？若存在，判断它是何种特殊平行四边形，并求出它面积的最值；若不存在，请说明理由．
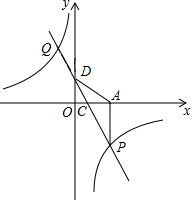8．如图，一次函数y=kx+1图象与反比例函数y=$\frac{m}{x}$的图象交于P、Q两点，过点P作PA⊥x轴，一次函数图象分别交x轴、y轴于C、D两点，$\frac{CD}{CP}$=$\frac{1}{3}$，且A（4，0）．
（1）求一次函数和反比例函数的表达式；
（2）求△ADP的面积；
（3）求反比例函数值大于一次函数值时，自变量x的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网