题目内容
4．
如图，梯形ABCD中，AB∥CD，∠D=（ ）| A． | 120° | B． | 135° | C． | 145° | D． | 155° |
分析 由AB∥CD，得到∠A+∠D=180°，把∠A的度数代入即可求出答案．
解答 解：∵AB∥CD，
∴∠A+∠D=180°，
∵∠A=45°，
∴∠D=180°-45°=135°，
故选：B．
点评 本题主要考查了梯形的性质，平行线的性质等知识点，解此题的关键是根据平行线的性质得到∠A+∠D=180°．
练习册系列答案
相关题目
14．
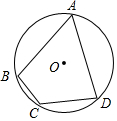如图，已知⊙O为四边形ABCD的外接圆，O为圆心，若∠BCD=120°，AB=AD=2，则⊙O的半径长为（ ）
如图，已知⊙O为四边形ABCD的外接圆，O为圆心，若∠BCD=120°，AB=AD=2，则⊙O的半径长为（ ）| A． | $\frac{3\sqrt{2}}{2}$ | B． | $\frac{\sqrt{6}}{2}$ | C． | $\frac{3}{2}$ | D． | $\frac{2\sqrt{3}}{3}$ |
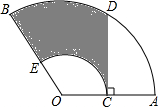如图，在扇形OAB中，C是OA的中点，CD⊥OA，CD与$\widehat{AB}$交于点D，以O为圆心，OC的长为半径作$\widehat{CE}$交OB于点E，若OA=4，∠AOB=120°，则图中阴影部分的面积为$\frac{4}{3}$π+2$\sqrt{3}$．（结果保留π）
12．若x1，x2是一元二次方程x2-2x-3=0的两个根，则x1•x2的值是（ ）
| A． | 2 | B． | -2 | C． | 4 | D． | -3 |
如图，在正方形ABCD中，等边三角形AEF的顶点E、F分别在边BC和CD上，则∠AEB=75度．
16．
如图是某个几何体的展开图，该几何体是（ ）
如图是某个几何体的展开图，该几何体是（ ）| A． | 三棱柱 | B． | 圆锥 | C． | 四棱柱 | D． | 圆柱 |