题目内容
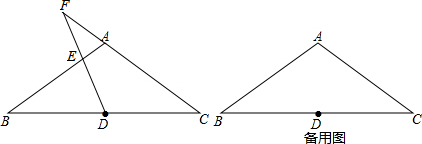
15．
如图，把△ABC沿虚线剪一刀，若∠A=43°，则∠1+∠2=223°．
分析 首先根据三角形内角和可以计算出∠C+∠B的度数，再根据四边形内角和为360°可算出∠1+∠2的结果．
解答 解：∵△ABC中，∠A=43°，
∴∠C+∠B=180°-∠A=137°，
∵∠C+∠B+∠1+∠2=360°，
∴∠1+∠2=360°-137°=223°．
故答案为：223°．
点评 此题主要考查了三角形内角和以及多边形内角和，关键是掌握多边形内角和定理：（n-2）．180° （n≥3）且n为整数）．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示，过六边形的顶点A的所有对角线可将六边形分成4个三角形．
3．
如图，A、B、C三点都在⊙O上，∠B=40°，∠C=20°，∠BOC的度数是（ ）
如图，A、B、C三点都在⊙O上，∠B=40°，∠C=20°，∠BOC的度数是（ ）| A． | 140° | B． | 100° | C． | 80° | D． | 120° |
如图，AD、AC分别是⊙O的直径和弦，且∠CAD=30°，OB⊥AD，交AC于点B．若OB=5，则弦AC的长等于15．
20．已知y是x的一次函数，下表列出了部分对应值，则n=3．
| x | -2 | 0 | 1 |
| y | -3 | 1 | n |
7．有下列说法：①如果两直线都与第三条直线平行，那么这两条直线也互相平行．②直线外一点到这条直线的垂线段，叫做点到直线的距离．③△ABC在平移过程中周长不变．④三角形的中线、角平分线、高线都在三角形内部．其中正确的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
4．菱形中较长的对角线与边长的比为$\sqrt{3}：1$，则菱形的四个角为（ ）
| A． | 30°，30°，150°，150° | B． | 45°，45°，135°，135° | ||
| C． | 60°，60°，120°，120° | D． | 90°，90°，90°，90° |
