题目内容
4.菱形中较长的对角线与边长的比为$\sqrt{3}:1$,则菱形的四个角为( )| A. | 30°,30°,150°,150° | B. | 45°,45°,135°,135° | ||
| C. | 60°,60°,120°,120° | D. | 90°,90°,90°,90° |
分析 由菱形对角线互相平分得出OA:AD=$\frac{\sqrt{3}}{2}$,得出∠ADO=60°,再由菱形对角线平分一组对角即可得出结果.
解答 解:如图所示: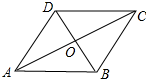
∵四边形ABCD是菱形,
∴AC⊥BD,OA=$\frac{1}{2}$AC,
∵AC:AD=$\sqrt{3}$:1.
∴OA:AD=$\frac{\sqrt{3}}{2}$:1=$\frac{\sqrt{3}}{2}$,
∴sin∠ADO=$\frac{OA}{AD}$=$\frac{\sqrt{3}}{2}$,
∴∠ADO=60°,
∴∠ABC=∠ADC=120°,
∴∠BAD=∠BCD=60°,
故选:C.
点评 本题考查了菱形的性质、锐角三角函数的运用;熟记菱形的性质和特殊角的三角函数值是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.已知$m=\sqrt{2}+1$,$n=\sqrt{2}-1$,则$\sqrt{{m^2}+{n^2}-3mn}$=( )
| A. | 9 | B. | $\sqrt{3}$ | C. | 3 | D. | 5 |
 如图,把△ABC沿虚线剪一刀,若∠A=43°,则∠1+∠2=223°.
如图,把△ABC沿虚线剪一刀,若∠A=43°,则∠1+∠2=223°. 如图,一次函数y=$\frac{1}{2}$x+5的图象与反比例函数y=-$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(-2,b),B两点.
如图,一次函数y=$\frac{1}{2}$x+5的图象与反比例函数y=-$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(-2,b),B两点.
 如图,在△ABC中,∠ACB=105°,AC边上的垂直平分线交AB边于点D,交AC边于点E,连结CD.
如图,在△ABC中,∠ACB=105°,AC边上的垂直平分线交AB边于点D,交AC边于点E,连结CD.