题目内容
10. 如图,AD、AC分别是⊙O的直径和弦,且∠CAD=30°,OB⊥AD,交AC于点B.若OB=5,则弦AC的长等于15.
如图,AD、AC分别是⊙O的直径和弦,且∠CAD=30°,OB⊥AD,交AC于点B.若OB=5,则弦AC的长等于15.
分析 首先连接CD,由∠CAD=30°,OB⊥AD,OB=5,即可求得OA的长,继而求得直径AD的长,继而求得答案.
解答  解:连接CD,
解:连接CD,
∵∠CAD=30°,OB⊥AD,OB=5,
∴OA=$\frac{OB}{tan30°}$=5$\sqrt{3}$,
∴AD=2OA=10$\sqrt{3}$,
∵AD是直径,
∴∠ACD=90°,
∴AC=AD•cos30°=10$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=15.
故答案为:15.
点评 此题考查了圆周角定理以及三角函数等知识.注意直径对的圆周角是直角,作出辅助线是关键.

练习册系列答案
相关题目
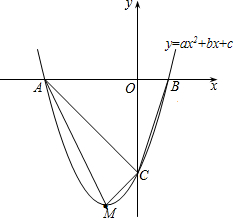 如图,抛物线y=ax2+bx+c的开口向上,顶点M在第三象限,抛物线与x轴交于A、B 两点,与y轴负半轴交于点C,点A坐标为(-3,0),点B坐标为(1,0).
如图,抛物线y=ax2+bx+c的开口向上,顶点M在第三象限,抛物线与x轴交于A、B 两点,与y轴负半轴交于点C,点A坐标为(-3,0),点B坐标为(1,0).
 如图,把△ABC沿虚线剪一刀,若∠A=43°,则∠1+∠2=223°.
如图,把△ABC沿虚线剪一刀,若∠A=43°,则∠1+∠2=223°.