题目内容
3．
如图，A、B、C三点都在⊙O上，∠B=40°，∠C=20°，∠BOC的度数是（ ）| A． | 140° | B． | 100° | C． | 80° | D． | 120° |
分析 首先连接OA，由等腰三角形的性质，可求得∠BAC的度数，然后由圆周角定理，求得∠BOC的度数．
解答 
解：连接OA，
∵OA=OB=OC，
∴∠OAC=∠C=20°，∠OAB=∠B=40°，
∴∠BAC=∠OAC+∠OAB=60°，
∴∠BOC=2∠BAC=120°．
故选D．
点评 此题考查了圆周角定理以及等腰三角形的性质．作出辅助线是关键．
练习册系列答案
相关题目
如图，把△ABC沿虚线剪一刀，若∠A=43°，则∠1+∠2=223°．
如图，一次函数y=$\frac{1}{2}$x+5的图象与反比例函数y=-$\frac{k}{x}$（k为常数，且k≠0）的图象交于A（-2，b），B两点．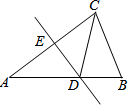
如图，在△ABC中，∠ACB=105°，AC边上的垂直平分线交AB边于点D，交AC边于点E，连结CD．