��Ŀ����
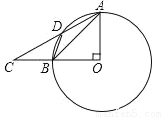
��ͼ����AOB=90�㣬C��OB���ӳ����ϣ�DΪ��O��һ�㣬��BAD=��BDC��
��1����֤��CD�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ1����OB=BC�����ı���AOBD�������
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
��ͼ����AOB=90�㣬C��OB���ӳ����ϣ�DΪ��O��һ�㣬��BAD=��BDC��
��1����֤��CD�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ1����OB=BC�����ı���AOBD�������
