题目内容
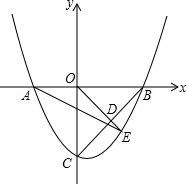 如图,对称轴为直线x=
如图,对称轴为直线x=| 1 |
| 2 |
(1)求A、B两点的坐标及该抛物线对应的解析式;
(2)D为BC的中点,延长OD与抛物线在第四象限内交于点E,连结AE、BE.
①求点E的坐标;
②判断ABE的形状,并说明理由;
(3)在x轴下方的抛物线上,是否存在一点P,使得四边形OBEP是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)首先求出A,B点坐标,进而利用待定系数法求二次函数解析式得出即可;
(2)①首先求出直线OE的解析式,进而与二次函数联立求出交点坐标即可;
②首先求出AE,BE的长,再利用勾股定理逆定理得出ABE的形状;
(3)利用平行四边形的性质与判定得出P点位置,进而得出P点坐标.
(2)①首先求出直线OE的解析式,进而与二次函数联立求出交点坐标即可;
②首先求出AE,BE的长,再利用勾股定理逆定理得出ABE的形状;
(3)利用平行四边形的性质与判定得出P点位置,进而得出P点坐标.
解答:解:(1)∵点A、B关于对称轴x=
对称,且AB=5
∴A(-2,0),B(3,0),
设抛物线的解析式为:y=ax2+bx+c,
把A(-2,0)B(3,0)C(0,-3)代入得:
,
解得:
,
∴该二次函数的解析式为:y=
x2-
x-3;
(2)①BC的中点D的坐标为(
,-
),
设直线OE的解析式为:y=kx,
把 D(
,-
),代入得:k=-1,
∴OE:y=-x,
由
,
得
,
∴E(2,-2),
②∵AE=
=
,BE=
=
,AB=5,
∴AB2=AE2+BE2,
∴△ABE是直角三角形;
(3)存在满足条件的点P
过E作PE∥OB,交抛物线于点P,得: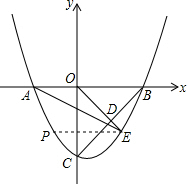
点P、E关于对称轴x=
对称
∴P的纵坐标为-2,
由
x2-
x-3=-2得
x1=-1,x2=2,
∴P(-1,-2),
∴PE=3=OB,
∴四边形OBEP是平行四边形,
∴存在点P,使四边形OBEP是平行四边形,坐标为(-1,-2).
| 1 |
| 2 |
∴A(-2,0),B(3,0),
设抛物线的解析式为:y=ax2+bx+c,
把A(-2,0)B(3,0)C(0,-3)代入得:
|
解得:
|
∴该二次函数的解析式为:y=
| 1 |
| 2 |
| 1 |
| 2 |
(2)①BC的中点D的坐标为(
| 3 |
| 2 |
| 3 |
| 2 |
设直线OE的解析式为:y=kx,
把 D(
| 3 |
| 2 |
| 3 |
| 2 |
∴OE:y=-x,
由
|
得
|
|
∴E(2,-2),
②∵AE=
| 42+22 |
| 20 |
| 12+22 |
| 5 |
∴AB2=AE2+BE2,
∴△ABE是直角三角形;
(3)存在满足条件的点P
过E作PE∥OB,交抛物线于点P,得:

点P、E关于对称轴x=
| 1 |
| 2 |
∴P的纵坐标为-2,
由
| 1 |
| 2 |
| 1 |
| 2 |
x1=-1,x2=2,
∴P(-1,-2),
∴PE=3=OB,
∴四边形OBEP是平行四边形,
∴存在点P,使四边形OBEP是平行四边形,坐标为(-1,-2).
点评:此题主要考查了二次函数综合以及平行四边形的判定与性质和勾股定理的逆定理以及待定系数法求二次函数解析式等知识,利用数形结合得出E点坐标是解题关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目

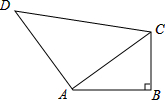 如图,∠B=90°,AB=4cm,BC=3cm,AD=12cm,CD=13cm,求四边形ABCD的面积.
如图,∠B=90°,AB=4cm,BC=3cm,AD=12cm,CD=13cm,求四边形ABCD的面积.
 如图,直线AB、CD相交于点O,∠AOD=80°,OE平分∠BOC,求∠AOE的度数.
如图,直线AB、CD相交于点O,∠AOD=80°,OE平分∠BOC,求∠AOE的度数.