题目内容
 如图,直线AB、CD相交于点O,∠AOD=80°,OE平分∠BOC,求∠AOE的度数.
如图,直线AB、CD相交于点O,∠AOD=80°,OE平分∠BOC,求∠AOE的度数.考点:对顶角、邻补角
专题:
分析:根据邻补角的性质,可得∠AOC的大小,根据对顶角相等,可得∠BOC的大小,根据角平分线的性质,可得∠COE的大小,根据角的和差,可得答案.
解答:解:由邻补角的性质得
∠AOC=180°-∠AOD=180°-80°=100°.
由对顶角相等得
∠BOC=∠AOD=80°,
由角平分线的性质得
∠COE=
∠BOC=
×80°=40°,
由角的和差得
∠AOE=∠AOC+∠COE=100°+40°=140°.
∠AOC=180°-∠AOD=180°-80°=100°.
由对顶角相等得
∠BOC=∠AOD=80°,
由角平分线的性质得
∠COE=
| 1 |
| 2 |
| 1 |
| 2 |
由角的和差得
∠AOE=∠AOC+∠COE=100°+40°=140°.
点评:本题考查了对顶角、邻补角,对顶角相等,邻补角互补是解题关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
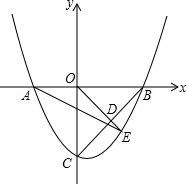 如图,对称轴为直线x=
如图,对称轴为直线x=
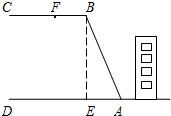 某居民楼后面紧邻着一个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为30米,坡角∠BAD=75°.为了减缓坡面防止山体滑坡,居委会决定对该斜坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.如果改造时保持坡脚A不动,坡顶B沿BC向左移15米到F点处,问这样改造能确保安全吗?(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,tan49°30′≈1.17,tan51°57′≈1.28)
某居民楼后面紧邻着一个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为30米,坡角∠BAD=75°.为了减缓坡面防止山体滑坡,居委会决定对该斜坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.如果改造时保持坡脚A不动,坡顶B沿BC向左移15米到F点处,问这样改造能确保安全吗?(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,tan49°30′≈1.17,tan51°57′≈1.28) 在△ABC中,AB=AC,∠BAC=90°.点D为线段BC上一动点,将线段DA绕点D顺时针旋转90°得到线段DE,连接CE,若AB=3CE,则tan∠BAD=
在△ABC中,AB=AC,∠BAC=90°.点D为线段BC上一动点,将线段DA绕点D顺时针旋转90°得到线段DE,连接CE,若AB=3CE,则tan∠BAD=