题目内容
15．解不等式组：$\left\{\begin{array}{l}{\frac{3x-1}{2}+\frac{x-2}{3}＜\frac{2x+2}{6}}\\{\frac{2-5x}{3}+1≤\frac{5x}{4}}\end{array}\right.$，并把解集在数轴上表示出来．分析 分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．
解答 解：解不等式$\frac{3x-1}{2}$+$\frac{x-2}{3}$＜$\frac{2x+2}{6}$，得：x＜1，
解不等式$\frac{2-5x}{3}$+1≤$\frac{5x}{4}$，得：x≥$\frac{4}{7}$，
∴不等式组的解集为$\frac{4}{7}$≤x＜1，
将解集表示在数轴上如下：
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
相关题目
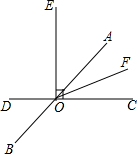如图所示，直线AB，CD相交于点O，OF平分∠AOC，EO⊥CD于点O，且∠DOF=160°，求∠BOE的度数．
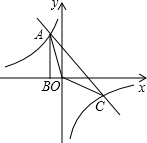如图，Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-（k+1）在第二象限的交点，AB⊥x轴于B，且S△ABO=$\frac{3}{2}$，求：
已知∠MAN和线段a，用尺规作等腰△ABC，使顶角为∠MAN，底边上的中线长为a，并写出所依据的主要定理．
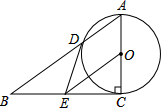如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，点E为BC的中点，连接DE．