题目内容
在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,DF为⊙O的切线,

(1)如图①,求∠DFC的度数;
(2)如图②,过点A作BC的平行线交BE的延长线于点G,连接CG,当△ABC时等边三角形时,求∠AGC的度数.

(1)如图①,求∠DFC的度数;
(2)如图②,过点A作BC的平行线交BE的延长线于点G,连接CG,当△ABC时等边三角形时,求∠AGC的度数.
考点:切线的性质,等边三角形的判定与性质,三角形中位线定理
专题:
分析:(1)连接AD,OD,根据等腰三角形的性质与平行线的性质,可得DF⊥OD,进而得出答案;
(2)根据题意,△ABC是等边三角形,可得BG是AC的垂直平分线,再根据平行线的性质,可得△ACG是等边三角形,故∠AGC=60°.
(2)根据题意,△ABC是等边三角形,可得BG是AC的垂直平分线,再根据平行线的性质,可得△ACG是等边三角形,故∠AGC=60°.
解答: 解:(1)连接AD,OD,
解:(1)连接AD,OD,
∵AB是⊙O的直径,
∴AD⊥BC.
∵AB=AC,
∴BD=DC,
又∵AO=BO,
∴OD是△ABC的中位线,
∴OD∥AC.
∵DF⊥AC,
∴DF⊥OD,
∴DF是⊙O的切线,
∴ODF=90°,
∴∠DFC=90°;
(2)∵AB是⊙O的直径,
∴BG⊥AC.
∵△ABC是等边三角形,
∴BG是AC的垂直平分线,
∴GA=GC.
又∵AG∥BC,∠ACB=60°,
∴∠CAG=∠ACB=60°.
∴△ACG是等边三角形.
∴∠AGC=60°.
 解:(1)连接AD,OD,
解:(1)连接AD,OD,∵AB是⊙O的直径,
∴AD⊥BC.
∵AB=AC,
∴BD=DC,
又∵AO=BO,
∴OD是△ABC的中位线,
∴OD∥AC.
∵DF⊥AC,
∴DF⊥OD,
∴DF是⊙O的切线,
∴ODF=90°,
∴∠DFC=90°;
(2)∵AB是⊙O的直径,
∴BG⊥AC.
∵△ABC是等边三角形,
∴BG是AC的垂直平分线,
∴GA=GC.
又∵AG∥BC,∠ACB=60°,
∴∠CAG=∠ACB=60°.
∴△ACG是等边三角形.
∴∠AGC=60°.
点评:本题考查常见的几何题型,包括切线的判定,及角度的大小的求法,要求学生掌握常见的解题方法,并能结合图形选择简单的方法解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图,二次函数y=a(x2-2mx-3m2)(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B的左侧),与y轴交于C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD,过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
如图,二次函数y=a(x2-2mx-3m2)(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B的左侧),与y轴交于C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD,过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
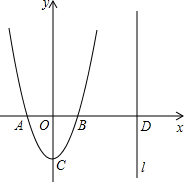 如图,二次函数y=ax2+c的图象交x轴于A、B两点,点A坐标为(-1,0),顶点C的坐标为(0,-2),点D在x轴上,过点D作直线l垂直于x轴,设点D的横坐标为m(m>1).
如图,二次函数y=ax2+c的图象交x轴于A、B两点,点A坐标为(-1,0),顶点C的坐标为(0,-2),点D在x轴上,过点D作直线l垂直于x轴,设点D的横坐标为m(m>1).