题目内容
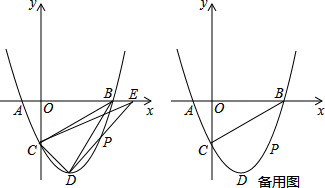
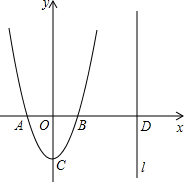 如图,二次函数y=ax2+c的图象交x轴于A、B两点,点A坐标为(-1,0),顶点C的坐标为(0,-2),点D在x轴上,过点D作直线l垂直于x轴,设点D的横坐标为m(m>1).
如图,二次函数y=ax2+c的图象交x轴于A、B两点,点A坐标为(-1,0),顶点C的坐标为(0,-2),点D在x轴上,过点D作直线l垂直于x轴,设点D的横坐标为m(m>1).(1)求二次函数的函数关系式和点B的坐标;
(2)二次函数y=ax2+c的图象上有一点Q,当△ODQ是以点D为直角顶点的等腰直角三角形时,求m的值;
(3)在直线l上有一点P(点P在第一象限),使得以点P、D、B为顶点的三角形与以点B、C、O为顶点的三角形全等,求点P的坐标.
考点:二次函数综合题
专题:
分析:(1)将点A和点C的坐标代入y=ax2+c,求出a和c的值,继而可求得函数关系式和点B的坐标;
(2)根据△ODQ是以点D为直角顶点的等腰直角三角形,可得点Q的坐标为(m,2m2-2),然后根据等腰直角三角形,可得出方程,求出m的值即可;
(3)分当△BOC≌△PDB时和当△BOC≌△BDP时,根据全等三角形的性质,求出点P的坐标.
(2)根据△ODQ是以点D为直角顶点的等腰直角三角形,可得点Q的坐标为(m,2m2-2),然后根据等腰直角三角形,可得出方程,求出m的值即可;
(3)分当△BOC≌△PDB时和当△BOC≌△BDP时,根据全等三角形的性质,求出点P的坐标.
解答:解:(1)∵二次函数y=ax2+c图象经过点A(-1,0)和点C(0,-2),
∴
,
解得:
,
∴二次函数的函数关系式为y=2x2-2;
∵点B与点A(-1,0)关于y轴对称,
∴点B的坐标为(1,0);
(2)当△ODQ是以点D为直角顶点的等腰直角三角形时,
点Q为二次函数和直线l的交点,
∵OD=m,
∴点Q的坐标为(m,2m2-2),
则2m2-2=m,
解得:m1=
,m2=
,
∵m>1,
∴m=
;
(3)①当△BOC≌△PDB时,PD=OB=1,BD=OC=2,
∴m=3,
∴点P的坐标为(3,1),
②当△BOC≌△BDP时,PD=OC=2,BD=OB=1,
∴m=2,
∴点P的坐标为(2,2).
∴
|
解得:
|
∴二次函数的函数关系式为y=2x2-2;
∵点B与点A(-1,0)关于y轴对称,
∴点B的坐标为(1,0);
(2)当△ODQ是以点D为直角顶点的等腰直角三角形时,
点Q为二次函数和直线l的交点,
∵OD=m,
∴点Q的坐标为(m,2m2-2),
则2m2-2=m,
解得:m1=
1-
| ||
| 4 |
1+
| ||
| 4 |
∵m>1,
∴m=
1+
| ||
| 4 |
(3)①当△BOC≌△PDB时,PD=OB=1,BD=OC=2,
∴m=3,
∴点P的坐标为(3,1),
②当△BOC≌△BDP时,PD=OC=2,BD=OB=1,
∴m=2,
∴点P的坐标为(2,2).
点评:本题是二次函数的综合题型,其中涉及到等腰直角三角形的性质,运用待定系数法求二次函数的解析式,函数图象上点的坐标特征,全等三角形的性质.此题综合性很强,解题的关键是方程思想,分类讨论思想与数形结合思想的应用.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
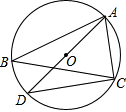 如图所示,已知⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD.若AD=5,AC=4,则cosB的值为( )
如图所示,已知⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD.若AD=5,AC=4,则cosB的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|

 如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100(
如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100(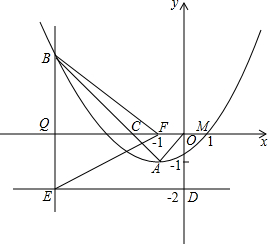 如图,抛物线y=ax2+bx+c(a≠0)的顶点为A(-1,-1),与x轴交点M(1,0).C为x轴上一点,且∠CAO=90°,线段AC的延长线交抛物线于B点,另有点F(-1,0).
如图,抛物线y=ax2+bx+c(a≠0)的顶点为A(-1,-1),与x轴交点M(1,0).C为x轴上一点,且∠CAO=90°,线段AC的延长线交抛物线于B点,另有点F(-1,0). 已知二次函数y=x2+bx+c,其图象抛物线交x轴于点A(1,0),B(3,0),交y轴于点C,直线l过点C,且交抛物线于另一点E(点E不与点A、B重合).
已知二次函数y=x2+bx+c,其图象抛物线交x轴于点A(1,0),B(3,0),交y轴于点C,直线l过点C,且交抛物线于另一点E(点E不与点A、B重合).