题目内容

若正整数n使得在计算n+（n+1）+（n+2）的过程中，各数位均不产生进位现象，则称n为“本位数”．例如：2和30是“本位数”，而5和91不是“本位数”．在不超过100的所有本位数中，全体奇数的和为
 
．
考点：规律型：数字的变化类
专题：
分析：先确定出所有大于0且小于100的“本位数”，再进一步计算即可得解．
解答：解：所有大于0且小于100的“本位数”有：1、2、10、11、12、20、21、22、30、31、32，
奇数有1、11、21、31，和为1+11+21+31=64．
故答案为：64．
点评：此题考查数字的变化规律，解决此题的关键是理解本位数的意义．
练习册系列答案
相关题目
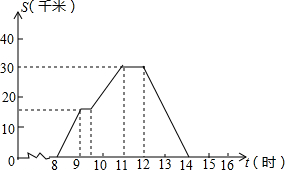一天上午8：00时，小华去县城购物，到下午14：00时返回家，设他离家的距离为s千米，结合图象回答：
（1）小华何时第一次休息？
（2）小华离家最远的距离是多少？
（3）在13：00时，小华离家的距离是多少？
（4）返回时平均速度是多少？
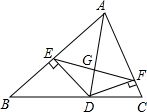已知：如图，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别是E，F，EF交AD于点G．
（1）判断AD与EF的位置关系，并加以说明理由．
（2）若AE=
5
，DE=2，求EF的长．
化简：
（1）
x2
x-1
+
x
1-x
；
（2）
2
a-1
+
a+3
1-a2
；
（3）
16-a2
a2+4a+4
÷
a-4
2a+4
•
a+2
a+4
；
（4）(
x+8
x2-4x+4
-
1
2-x
)÷
x+3
x2-2x
．
在平面直角坐标系中，一蚂蚁从原点O出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位．其行走路线如图所示．

（1）填写下列各点的坐标：
A1（
 
，
 
），A3（
 
，
 
），A12（
 
，
 
）；
（2）写出点A4n的坐标（n是正整数）：A4n（
 
，
 
）；
（3）蚂蚁从点A2013到A2014的移动方向是
 
．
在图中，这些方砖除颜色外完全相同，小老鼠在方砖上自由走动，最终停在白色方砖上的概率为
 
．
多项式x2-4与x2-4x+4有相同的因式是
 
．
一元二次方程-
1
2
x2+4x=3的二次项系数和常数项的乘积为
 
．
如图，以AB（长为3cm）为直径的圆（O1为圆心），沿直线l向右平移4cm到如图所示的位置（O2为圆心），则图中阴影部分的面积为
 
cm2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网