题目内容
13.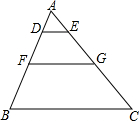 如图,在△ABC中,DE∥FG∥BC,且AD:DF:BF=2:3:4,已知△ABC的周长为27,BC=9,则四边形DEGF的周长为11.
如图,在△ABC中,DE∥FG∥BC,且AD:DF:BF=2:3:4,已知△ABC的周长为27,BC=9,则四边形DEGF的周长为11.
分析 由AD:DF:BF=2:3:4,得到AD:AF:AB=2:5:9,由于DE∥FG∥BC,于是得到△ADE∽△AFG∽△ABC,通过比例式得到DE=2,FG=5,于是求得△ADE的周长=6,△AFG的周长=15,得到AD+AE=4,即可得到结果.
解答 解:∵AD:DF:BF=2:3:4,
∴AD:AF:AB=2:5:9,
∵DE∥FG∥BC,
∴△ADE∽△AFG∽△ABC,
∴$\frac{AD}{AB}=\frac{DE}{BC}$=$\frac{2}{9}$,$\frac{AF}{AB}=\frac{FG}{BC}$=$\frac{5}{9}$,
∴DE=2,FG=5,
∴△ADE的周长:△ABC的周长=$\frac{2}{9}$,∴△AFG的周长:△ABC的周长=$\frac{5}{9}$,
∵△ABC的周长为27,
∴△ADE的周长=6,△AFG的周长=15,
∴AD+AE=4,
∴四边形DEGF的周长为:15-4=11,
故答案为:11.
点评 本题考查了相似三角形的判定和性质,三角形的周长的求法,熟练掌握相似三角形的判定和性质定理是解题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
18.已知a+b-2=0,那么$\frac{b}{{a}^{2}-{b}^{2}}$+$\frac{a}{{b}^{2}-{a}^{2}}$的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
2.若三角形两边的长分别是8和6,第三边的长是方程x2-2x=10(x-2)的一个实数根,则这个三角形的周长是( )
| A. | 24 | B. | 24或16 | C. | 16 | D. | 22 |
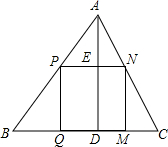 用一个大小形状固定的不等边锐角三角形纸,剪出一个最大的正方形纸备用.
用一个大小形状固定的不等边锐角三角形纸,剪出一个最大的正方形纸备用. 如图所示的是某台阶的一部分,各级台阶的高度与宽度相等.如果点A的坐标为(0,0),点B的坐标为(1,1).
如图所示的是某台阶的一部分,各级台阶的高度与宽度相等.如果点A的坐标为(0,0),点B的坐标为(1,1).