题目内容
1. 如图所示的是某台阶的一部分,各级台阶的高度与宽度相等.如果点A的坐标为(0,0),点B的坐标为(1,1).
如图所示的是某台阶的一部分,各级台阶的高度与宽度相等.如果点A的坐标为(0,0),点B的坐标为(1,1).(1)请建立适当的平面直角坐标系.并写出点C,D,E,F的坐标;
(2)说明点B,C,D,E,F的坐标与点A的坐标相比较有什么变化?
(3)如果台阶有10级,要在台阶上铺设地毯,地毯的长度至少多长?
分析 (1)利用A,B点坐标进而得出对应点坐标即可;
(2)利用1)中所求得出各点坐标变化规律;
(3)利用(1)中所求得出对应点坐标进而得出地毯的长度.
解答  解:(1)如图所示:点C(2,2),D(3,3),E(4,4),F(5,5);
解:(1)如图所示:点C(2,2),D(3,3),E(4,4),F(5,5);
(2)点B,C,D,E,F的坐标与点A的坐标相比横坐标相等,且是连续的正整数;
(3)由题意可得:第10级台阶的高度为10,相应对应点坐标为:(10,10),
则要在台阶上铺设地毯,地毯的长度至少:10+10=20.
点评 此题主要考查了坐标与图形的性质,根据题意得出对应点坐标是解题关键.

练习册系列答案
相关题目
12.把一元二次方程6x2-3=4x(2x-1)化为一般形式是( )
| A. | -2x2-4x+3=0 | B. | 2x2+4x-3=0 | C. | 2x2-4x+3=0 | D. | 2x2-4x-3=0 |
16.下列实数中是无理数的是( )
| A. | $\frac{22}{7}$ | B. | 2-2 | C. | 5.$\stackrel{••}{15}$ | D. | sin 45° |
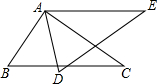 如图,△ABC≌△ADE,则下列结论成立的是( )
如图,△ABC≌△ADE,则下列结论成立的是( )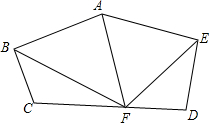 如图,已知AB=AE,BC=ED,∠C=∠D,点F是CD的中点,∠BAF与∠EAF相等吗?为什么?
如图,已知AB=AE,BC=ED,∠C=∠D,点F是CD的中点,∠BAF与∠EAF相等吗?为什么?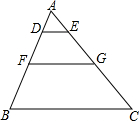 如图,在△ABC中,DE∥FG∥BC,且AD:DF:BF=2:3:4,已知△ABC的周长为27,BC=9,则四边形DEGF的周长为11.
如图,在△ABC中,DE∥FG∥BC,且AD:DF:BF=2:3:4,已知△ABC的周长为27,BC=9,则四边形DEGF的周长为11.