题目内容
8.已知关于x的一元二次方程x2-2x+m+2=0有两个不等的实数根x1和x2(1)求m的取值范围并证明x1x2=m+2;
(2)若|x1-x2|=2,求m的值.
分析 (1)根据判别式的意义得到△=(-2)2-4(m+2)=-4m-4>0解得m<-1,再利用求根公式解方程,然后计算x1x2;
(2)先根据根与系数的关系得x1+x2=2,x1x2=m+2,再把|x1-x2|=2两边平方得到(x1-x2)2=4,接着利用完全平方公式变形得到(x1+x2)2-4x1x2=4,所以4-4(m+2)=4,
然后解关于m的方程即可.
解答 解:(1)∵关于x的一元二次方程x2-2x+m+2=0有两个不等的实数根x1和x2,
所以△=(-2)2-4(m+2)=-4m-4>0
解得m<-1,
根据求根公式${x_1}=1+\sqrt{-m-1}$,${x_2}=1-\sqrt{-m-1}$
∴${x_1}{x_2}=1-{({\sqrt{-m-1}})^2}=m+2$;
(2)根据根与系数的关系得x1+x2=2,x1x2=m+2,
∵|x1-x2|=2,
∴(x1-x2)2=4,
∴(x1+x2)2-4x1x2=4,
∴4-4(m+2)=4,
解得m=-2.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

练习册系列答案
相关题目
16.下列实数中是无理数的是( )
| A. | $\frac{22}{7}$ | B. | 2-2 | C. | 5.$\stackrel{••}{15}$ | D. | sin 45° |
3. 如图所示几何体的几何体的主视图是( )
如图所示几何体的几何体的主视图是( )
 如图所示几何体的几何体的主视图是( )
如图所示几何体的几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
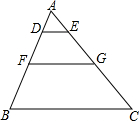 如图,在△ABC中,DE∥FG∥BC,且AD:DF:BF=2:3:4,已知△ABC的周长为27,BC=9,则四边形DEGF的周长为11.
如图,在△ABC中,DE∥FG∥BC,且AD:DF:BF=2:3:4,已知△ABC的周长为27,BC=9,则四边形DEGF的周长为11. 如图所示,△ABC中,D点在AC上,E点在BC上,且满足△ABD≌△EBD,△DBE≌△DCE,求∠A和∠C的度数.
如图所示,△ABC中,D点在AC上,E点在BC上,且满足△ABD≌△EBD,△DBE≌△DCE,求∠A和∠C的度数.