Question

4．如图，△ABC为一个直角三角形的空地，∠C为直角，AC边长为3百米，BC边长为4百米，现决定在空地内筑一条笔直的路EF（宽度不计），E为BC的中点，F为三角形ABC边上的一点，且EF将该空地分成一个四边形和一个三角形，若分成的四边形和三角形周长相等，求此时小路EF的长度．

Answer 1

分析 根据勾股定理得AB=5，由中点的性质得BE=EC=2，①当点F在AB上时，设BF=x，则AF=5-x，根据四边形和三角形周长相等可求得x的值，作EG⊥BF，由sinB=$\frac{AC}{AB}$=$\frac{3}{5}$、cosB=$\frac{BC}{AB}$=$\frac{4}{5}$求得BG=BEcosB=$\frac{8}{5}$、GE=BEsinB=$\frac{6}{5}$、GF=BF-BG=$\frac{12}{5}$，根据勾股定理可得EF；②当点F在AC上时，设CF=a，则AF=3-a，由四边形和三角形周长相等可求得a的值，根据AF=3-a=-1可排除此种情况．

解答 解：∵AC=3，BC=4，∠C=90°，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5，
∵E为BC的中点，
∴BE=EC=2，
①如图1，当点F在AB上时，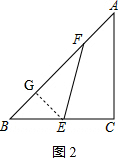

设BF=x，则AF=5-x，
∵BE+BF+EF=EC+AC+AF+EF，即2+x+EF=2+3+5-x+EF，
∴x=4，
过点E作EG⊥BF于点G，
∵sinB=$\frac{AC}{AB}$=$\frac{3}{5}$，cosB=$\frac{BC}{AB}$=$\frac{4}{5}$，
∴BG=BEcosB=2×$\frac{4}{5}$=$\frac{8}{5}$，GE=BEsinB=2×$\frac{3}{5}$=$\frac{6}{5}$，
∴GF=BF-BG=4-$\frac{8}{5}$=$\frac{12}{5}$，
则EF=$\sqrt{G{F}^{2}+G{E}^{2}}$=$\sqrt{（\frac{12}{5}）^{2}+（\frac{6}{5}）^{2}}$=$\frac{6\sqrt{5}}{5}$（百米）；
②如图2，当点F在AC上时，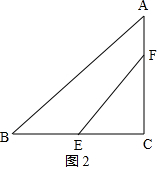

设CF=a，则AF=3-a，
∵EC+CF+EF=BE+EF+AF+AB，即2+a+EF=2+EF+3-a+5，
解得：a=4，
∴此时AF=3-a=-1，不符合题意，舍去；
综上可知，小路EF的长度为$\frac{6}{5}\sqrt{5}$百米．

点评 本题主要考查勾股定理的应用、解直角三角形等知识点，根据四边形与三角形的周长相等分类讨论并得到相关线段的长是解题的关键．