题目内容
14.先化简,再求值:$\frac{x^2}{x^2-1}÷(\frac{1-2x}{x-1}-x+1)$,其中x满足x2+3x=0.分析 先化简题目中的式子,然后根据x2+3x=0即可求得x的值,从而可以解答本题.
解答 解:$\frac{x^2}{x^2-1}÷(\frac{1-2x}{x-1}-x+1)$
=$\frac{{x}^{2}}{(x+1)(x-1)}÷\frac{(1-2x)-(x-1)(x-1)}{x-1}$
=$\frac{{x}^{2}}{(x+1)(x-1)}•\frac{x-1}{1-2x-{x}^{2}+1}$
=$-\frac{{x}^{2}}{(x+1)({x}^{2}+2x-2)}$,
∵x2+3x=0,
∴x2=-3x,x=0或x=-3,
∴原式=$-\frac{-3x}{(x+1)(-3x+2x-2)}$=$\frac{3x}{(x+1)(-x-2)}$=-$\frac{3x}{{x}^{2}+3x+2}$=-$\frac{3x}{2}$,
当x=0时,原式=0,
当x=-3时,原式=-$\frac{3}{2}×(-3)$=$\frac{9}{2}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
1.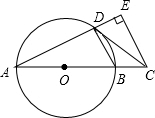 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.若CE=4,DE=2,则AD的长是( )
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.若CE=4,DE=2,则AD的长是( )
 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.若CE=4,DE=2,则AD的长是( )
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.若CE=4,DE=2,则AD的长是( )| A. | 2$\sqrt{2}$ | B. | 6 | C. | 3 | D. | 6$\sqrt{2}$ |
5.要使$\sqrt{\frac{8}{x-2}}$有意义,则x的取值范围是( )
| A. | x<2 | B. | x>2 | C. | x≤2 | D. | x>0且x≠2 |
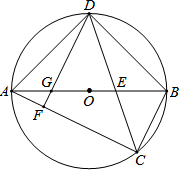 如图,AB为⊙O的直径,弦CD平分∠ACB,CD交OB于点E.DF⊥AC于点F,交AO于点G.
如图,AB为⊙O的直径,弦CD平分∠ACB,CD交OB于点E.DF⊥AC于点F,交AO于点G. 如图,在平行四边形ABCD中,添加一个条件使它成为一个矩形,你添的条件是AC=BD(不唯一).
如图,在平行四边形ABCD中,添加一个条件使它成为一个矩形,你添的条件是AC=BD(不唯一).