题目内容
19.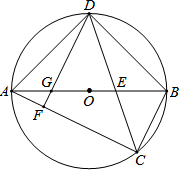 如图,AB为⊙O的直径,弦CD平分∠ACB,CD交OB于点E.DF⊥AC于点F,交AO于点G.
如图,AB为⊙O的直径,弦CD平分∠ACB,CD交OB于点E.DF⊥AC于点F,交AO于点G.(1)求证:△EDG∽△EAD;
(2)若EG=10,EA=16,求⊙O的半径
(3)求证:DF=BC+AF.
分析 (1)根据两角对应相等证明两三角形相似;
(2)作高线ME,先利用三角形相似求DE的长,由△DME是等腰直角三角形,分别求DM、ME、MG的长,因此得到DG的长,由(1)中的两三角形相似列比例式可求得AD的长,从而得到圆的直径,即可得到圆的半径长;
(3)如图2,作辅助线,构建两三角形全等,证明Rt△ADF≌Rt△BDH(HL),可得结论.
解答 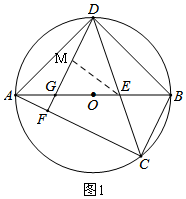 证明:(1)∵AB为⊙O的直径,
证明:(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∵弦CD平分∠ACB,
∴∠ACD=∠DCB=45°,
∵DF⊥AC,
∴∠DFC=90°,
∴∠EDG=45°,
∵∠DAB=∠DCB=45°,
∴∠DAB=∠EDG,
∵∠DEG=∠DEA,
∴△EDG∽△EAD;
(2)如图1,∵△EDG∽△EAD,
∴$\frac{ED}{EA}=\frac{EG}{ED}=\frac{DG}{AD}$,
∵EG=10,AE=16,
∴ED2=10×16=160,
∴ED=$±4\sqrt{10}$,
∴$\frac{DG}{AD}=\frac{4\sqrt{10}}{16}$=$\frac{\sqrt{10}}{4}$,
过E作EM⊥DF于M,
∴△DME是等腰直角三角形,
∴DM=EM=$\frac{4\sqrt{10}}{\sqrt{2}}$=4$\sqrt{5}$,
在Rt△MGE中,MG=$\sqrt{1{0}^{2}-(4\sqrt{5})^{2}}$=2$\sqrt{5}$,
∴DG=DM+MG=6$\sqrt{5}$,
∴$\frac{DG}{AD}=\frac{6\sqrt{5}}{AD}=\frac{\sqrt{10}}{4}$,
∴AD=12$\sqrt{2}$,
∵∠ACD=∠DCB=45°,
∴$\widehat{AD}=\widehat{BD}$,
∴AD=BD,
∵∠ADB=90°,
∴△ADB是等腰直角三角形,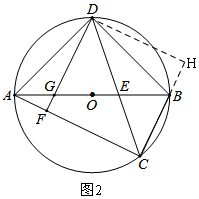
∴AB=$\sqrt{2}$AD=$\sqrt{2}$×$12\sqrt{2}$=24,
∴⊙O的半径是12;
(3)如图2,过D作DH⊥CB,交CB的延长线于H,
∵∠DFC=∠ACB=∠H=90°,
∴四边形DFCH是矩形,
∵DF=FC,
∴矩形DFCH是正方形,
∴DF=FC=CH=DH,
∵AD=BD,
∴Rt△ADF≌Rt△BDH(HL),
∴DF=CH=BC+BH=BC+AF.
点评 本题考查了圆周角定理、三角形相似和全等的性质和判定、勾股定理、正方形的性质和判定、等腰直角三角形的性质和判定,第二问有难度,构建辅助线是关键,利用相似和等腰直角三角形依次求边长,从而得结论,第三问是常考题型,构建两三角形全等是关键.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案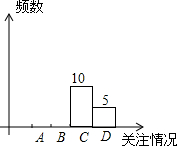 2017年,安徽省教育部门将对体育中考自选项目进行改革,某校为了解九年级学生对这次改革的看法,随机调查了部分九年级学生,并根据调查结果制作了如下不完整的统计图表.
2017年,安徽省教育部门将对体育中考自选项目进行改革,某校为了解九年级学生对这次改革的看法,随机调查了部分九年级学生,并根据调查结果制作了如下不完整的统计图表.根据以上提供的信息,解答下列问题:
(1)本次一共抽取了50名学生,k=10,m=25,n=0.2.
(2)补全频数分布直方图,并求这组数据的众数和中位数.
(3)若该校9年级共有学生2000名,请估计该校对体育中考改革关注(含高度关注和一般关注)的学生人数.
| 关注情况 | 频数 | 频率 |
| A.高度关注 | k | 0.2 |
| B.一般关注 | m | 0.5 |
| C.极少关注 | 10 | n |
| D.不关注 | 5 | 0.1 |
| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{2017}{2018}$ | D. | 1 |