题目内容
17. 如图,CD为⊙O直径,CD⊥AB于点F,AO⊥BC于E,AO=1cm,则阴影部分的面积为( )
如图,CD为⊙O直径,CD⊥AB于点F,AO⊥BC于E,AO=1cm,则阴影部分的面积为( )| A. | $\frac{1}{3}π$-$\frac{\sqrt{3}}{4}$cm2 | B. | $\frac{\sqrt{3}}{8}$cm2 | C. | $\frac{\sqrt{3}}{2}$cm2 | D. | $\sqrt{3}$cm2 |
分析 连结OB,根据垂径定理及圆周角定理得出∠AOB=2∠AOD=120°,OF=$\frac{1}{2}$AO=$\frac{1}{2}$,AB=2AF=$\sqrt{3}$,再由S阴影=S扇形OAB-S△OAB即可得出结论.
解答 解: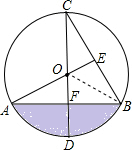 连结OB,
连结OB,
∵CD为直径,CD⊥AB,
∵AF=BF,$\widehat{AD}$=$\widehat{BD}$,
∴∠AOD=∠DOE=2∠C,
∵∠COE=∠AOF,
∴∠COE=2∠C.
∵AE⊥BC,
∴∠C=90°×$\frac{1}{3}$=30°,∠AOD=60°,
∵∠AOB=2∠AOD=120°,OF=$\frac{1}{2}$AO=$\frac{1}{2}$,AB=2AF=$\sqrt{3}$,
∴S扇形OAB=$\frac{120π×{1}^{2}}{360}$=$\frac{1}{3}$π,
S△OAB=$\frac{1}{2}$AB•OF=$\frac{1}{2}$×$\sqrt{3}$×$\frac{1}{2}$=$\frac{\sqrt{3}}{4}$,
∴S阴影=S扇形OAB-S△OAB=$\frac{1}{3}π$-$\frac{\sqrt{3}}{4}$.
故选A.
点评 本题考查的是扇形的面积,垂径定理,熟知垂径定理,圆周角定理及扇形的面积公式是解答此题的关键.

练习册系列答案
相关题目
8.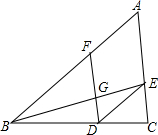 在△ABC中,D、F、E分别在边BC、AB、AC上一点,连接BE交FD于点G,若四边形AFDE是平行四边形,则下列说法错误的是( )
在△ABC中,D、F、E分别在边BC、AB、AC上一点,连接BE交FD于点G,若四边形AFDE是平行四边形,则下列说法错误的是( )
 在△ABC中,D、F、E分别在边BC、AB、AC上一点,连接BE交FD于点G,若四边形AFDE是平行四边形,则下列说法错误的是( )
在△ABC中,D、F、E分别在边BC、AB、AC上一点,连接BE交FD于点G,若四边形AFDE是平行四边形,则下列说法错误的是( )| A. | $\frac{AF}{AB}$=$\frac{EG}{BE}$ | B. | $\frac{FG}{GD}$=$\frac{BG}{GE}$ | C. | $\frac{FG}{AB}$=$\frac{DG}{BC}$ | D. | $\frac{AF}{BF}$=$\frac{AE}{BC}$ |
2.点A($\sqrt{2}$,1)关于y轴对称的点的坐标是( )
| A. | (-$\sqrt{2}$,-1) | B. | (-$\sqrt{2}$,1) | C. | ($\sqrt{2}$,-1) | D. | ($\sqrt{2}$,1) |
 如图,把一张长方形纸片ABCD沿EF折叠,C点落在C′处,D点落在D′处,ED′交BC于点G.已知∠EFG=50°.则∠BGD′的度数为80°.
如图,把一张长方形纸片ABCD沿EF折叠,C点落在C′处,D点落在D′处,ED′交BC于点G.已知∠EFG=50°.则∠BGD′的度数为80°. 如图,在10×10正方形网格中,每个小正方形的边长均为1个单位长度.点B、C坐标分别为(-4,2)、(-1,2).
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位长度.点B、C坐标分别为(-4,2)、(-1,2). 折叠矩形ABCD,使它的顶点D落在BC边上的F处,如图,AB=6,AD=10,那么CE的长为$\frac{8}{3}$.
折叠矩形ABCD,使它的顶点D落在BC边上的F处,如图,AB=6,AD=10,那么CE的长为$\frac{8}{3}$.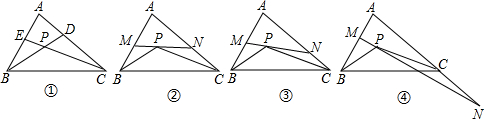
 如图,甲、乙两艘轮船同时从港口O出发,甲轮船以20海里/时的速度向南偏东45°方向航行,乙轮船向南偏西45°方向航行.已知它们离开港口O两小时后,两艘轮船相距50海里,求乙轮船平均每小时航行多少海里?
如图,甲、乙两艘轮船同时从港口O出发,甲轮船以20海里/时的速度向南偏东45°方向航行,乙轮船向南偏西45°方向航行.已知它们离开港口O两小时后,两艘轮船相距50海里,求乙轮船平均每小时航行多少海里?