题目内容
16. “小头爸爸”为了检查“大头儿子”对平行线的条件与性质这部分知识的掌握情况,给他出了一道题:如图,AB∥DE,∠B=80°,CM平分∠BCD,CN⊥CM,求∠NCE的度数.“大头儿子”稍加思索,就做出来了,你知道他是怎样解的吗?请把你的推理过程写下来吧.
“小头爸爸”为了检查“大头儿子”对平行线的条件与性质这部分知识的掌握情况,给他出了一道题:如图,AB∥DE,∠B=80°,CM平分∠BCD,CN⊥CM,求∠NCE的度数.“大头儿子”稍加思索,就做出来了,你知道他是怎样解的吗?请把你的推理过程写下来吧.
分析 先根据AB∥DE,得出∠B+∠DCB=180°,故可得出∠DCB的度数,再根据CM平分∠BCD,可知∠DCM=$\frac{1}{2}$∠BCD,由CM⊥CN,可知∠MCN=90°,根据∠ECN=180°-∠MCN-∠DCM即可得出结论.
解答 解:∵AB∥DE,∠B=80°
∴∠B+∠DCB=180°,
∴∠DCB=180°-80°=100°,
∵CM平分∠BCD,
∴∠DCM=$\frac{1}{2}$∠BCD=$\frac{1}{2}$×100°=50°,
∵CM⊥CN,
∴∠MCN=90°,
∴∠ECN=180°-90°-50°=40°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补.

练习册系列答案
相关题目
6.下列说法正确的是( )
| A. | -4是16的平方根 | B. | $\sqrt{16}$的算术平方根是4 | ||
| C. | 0没有算术平方根 | D. | 2的平方根是$\sqrt{2}$ |
8.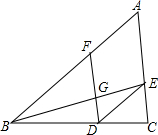 在△ABC中,D、F、E分别在边BC、AB、AC上一点,连接BE交FD于点G,若四边形AFDE是平行四边形,则下列说法错误的是( )
在△ABC中,D、F、E分别在边BC、AB、AC上一点,连接BE交FD于点G,若四边形AFDE是平行四边形,则下列说法错误的是( )
 在△ABC中,D、F、E分别在边BC、AB、AC上一点,连接BE交FD于点G,若四边形AFDE是平行四边形,则下列说法错误的是( )
在△ABC中,D、F、E分别在边BC、AB、AC上一点,连接BE交FD于点G,若四边形AFDE是平行四边形,则下列说法错误的是( )| A. | $\frac{AF}{AB}$=$\frac{EG}{BE}$ | B. | $\frac{FG}{GD}$=$\frac{BG}{GE}$ | C. | $\frac{FG}{AB}$=$\frac{DG}{BC}$ | D. | $\frac{AF}{BF}$=$\frac{AE}{BC}$ |
 如图,把一张长方形纸片ABCD沿EF折叠,C点落在C′处,D点落在D′处,ED′交BC于点G.已知∠EFG=50°.则∠BGD′的度数为80°.
如图,把一张长方形纸片ABCD沿EF折叠,C点落在C′处,D点落在D′处,ED′交BC于点G.已知∠EFG=50°.则∠BGD′的度数为80°.
 如图,在10×10正方形网格中,每个小正方形的边长均为1个单位长度.点B、C坐标分别为(-4,2)、(-1,2).
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位长度.点B、C坐标分别为(-4,2)、(-1,2).