题目内容
10.若不等式组$\left\{\begin{array}{l}{x-a<2}\\{b-2x<0}\end{array}\right.$的解集为-1<x<1,求a、b的值.分析 先求得不等式的解集(用含a,b的式子表示),然后列出关于a,b的方程即可求得a,b的值.
解答 解:解不等式组$\left\{\begin{array}{l}{x-a<2}\\{b-2x<0}\end{array}\right.$得:$\left\{\begin{array}{l}{x<2+a}\\{x>\frac{b}{2}}\end{array}\right.$,
因为不等式组$\left\{\begin{array}{l}{x-a<2}\\{b-2x<0}\end{array}\right.$的解集为-1<x<1,
可得:$\left\{\begin{array}{l}{2+a=1}\\{\frac{b}{2}=-1}\end{array}\right.$,
解得:a=1,b=-2.
点评 此题考查不等式的解集,关键是列出关于a,b的方程.

练习册系列答案
相关题目
20.圆周长公式C=2πR中,下列说法正确的是( )
| A. | π、R是变量,2为常量 | B. | C、R为变量,2、π为常量 | ||
| C. | R为变量,2、π、C为常量 | D. | C为变量,2、π、R为常量 |
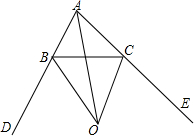 如图,△ABC的内角∠BAC的平分线和外角∠DBC的平分线交于点O,连接CO,求证:CO平分△ABC的外角∠BCE.
如图,△ABC的内角∠BAC的平分线和外角∠DBC的平分线交于点O,连接CO,求证:CO平分△ABC的外角∠BCE.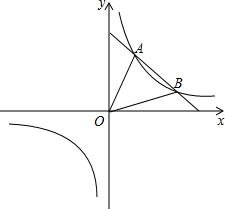 如图,点A、B是反比例函数y=$\frac{k}{x}$图象上的两点,已知点B的坐标为(3,2),△AOB的面积为2.5,求该反比例函数的解析式和点A的坐标.
如图,点A、B是反比例函数y=$\frac{k}{x}$图象上的两点,已知点B的坐标为(3,2),△AOB的面积为2.5,求该反比例函数的解析式和点A的坐标. 如图,在△ABC中,三个内角的角平分线交于点O,OF⊥BC于点E,若∠AOB=130°,求∠COF的度数.
如图,在△ABC中,三个内角的角平分线交于点O,OF⊥BC于点E,若∠AOB=130°,求∠COF的度数.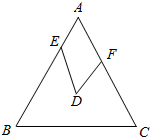 如图,已知点D是边长为1的等边三角形ABC的内心,点E,F分别在边AB,AC上,且满足∠EDF=60°,求△AEF的周长.
如图,已知点D是边长为1的等边三角形ABC的内心,点E,F分别在边AB,AC上,且满足∠EDF=60°,求△AEF的周长.