题目内容
3.在△ABC中,∠ABC=45°,AB=4$\sqrt{2}$,BD⊥BC,且BD=2,若AD⊥AC,则S△ABC=12或20.分析 分两种情况:(1)当A,D在BC同侧时,如图1所示,作AE⊥BD交BD的延长线于E,连结DC;(2)当A,D在BC异侧时,如图2所示,作AE⊥BD交BD的延长线于E,连结DC;根据四点共圆的性质,等腰直角三角形的性质,勾股定理得到DE,BC,再根据三角形面积公式即可求解.
解答 解:(1)当A,D在BC同侧时,如图1所示,作AE⊥BD交BD的延长线于E,连结DC,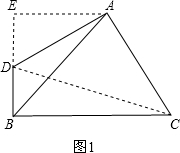 ∵BD⊥BC,AD⊥AC,
∵BD⊥BC,AD⊥AC,
∴A,D,B,C四点共圆,
∴∠ADC=∠ABC=45°=∠ABE,
∴△ADC和△ABE都是等腰直角三角形,
∵AB=4$\sqrt{2}$,
∴AE=BE=$\frac{\sqrt{2}}{2}$AB=$\frac{\sqrt{2}}{2}$×4$\sqrt{2}$=4,
∵BD=2,
∴DE=BE-BD=2,
∴AD2=AE2+DE2=42+22=20,
∴DC2=2AD2=40,
∴BC=$\sqrt{D{C}^{2}-B{D}^{2}}$=$\sqrt{40-4}$=6,
∴S△ABC=$\frac{1}{2}$BC•BE=12;
(2)当A,D在BC异侧时,如图2所示,作AE⊥BD交BD的延长线于E,连结DC,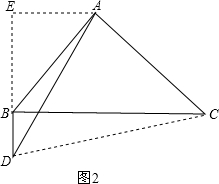 ∵BD⊥BC,AD⊥AC,
∵BD⊥BC,AD⊥AC,
∴A,D,B,C四点共圆,
∴∠ADC=∠ABC=45°=∠ABE,
∴△ADC和△ABE都是等腰直角三角形,
∵AB=4$\sqrt{2}$,
∴AE=BE=$\frac{\sqrt{2}}{2}$AB=$\frac{\sqrt{2}}{2}$×4$\sqrt{2}$=4,
∵BD=2,
∴DE=BE+BD=6,
∴AD2=AE2+DE2=42+62=52,
∴DC2=2AD2=104,
∴BC=$\sqrt{D{C}^{2}-B{D}^{2}}$=$\sqrt{104-4}$=10,
∴S△ABC=$\frac{1}{2}$BC•BE=20.
故S△ABC=12或20.
故答案为:12或20.
点评 考查了勾股定理,涉及的知识点有:四点共圆的性质,等腰直角三角形的性质,勾股定理,三角形面积,分类思想的运用,解题的关键是得到DE,BC的长.

 阅读快车系列答案
阅读快车系列答案| A. | 两个有理数相加,和一定比每个加数都大 | |
| B. | 两个有理数相加,只需把绝对值相加 | |
| C. | 两个有理数相加,和非正即负 | |
| D. | 两个有理数相加,必须确定和的符号和绝对值 |
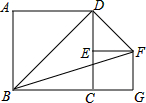 如图,菱形ABCD与菱形ECGF的顶点B、C、G在同一直线上,点E在线段CD上,AB=2,∠ABC=60°,则△BDF的面积为( )
如图,菱形ABCD与菱形ECGF的顶点B、C、G在同一直线上,点E在线段CD上,AB=2,∠ABC=60°,则△BDF的面积为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | 2$\sqrt{3}$ |
 如图,在△ABC中,三个内角的角平分线交于点O,OF⊥BC于点E,若∠AOB=130°,求∠COF的度数.
如图,在△ABC中,三个内角的角平分线交于点O,OF⊥BC于点E,若∠AOB=130°,求∠COF的度数.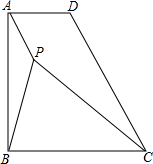 已知在直角梯形ABCD中,∠ABC=90°,AB=BC,点P是梯形内一点,且PA=1,PB=2,PC=3
已知在直角梯形ABCD中,∠ABC=90°,AB=BC,点P是梯形内一点,且PA=1,PB=2,PC=3 如图,小正方形网格边长均为1,△ABC顶点都在格点上,请你判断△ABC的形状是等腰直角三角形,请说明理由.
如图,小正方形网格边长均为1,△ABC顶点都在格点上,请你判断△ABC的形状是等腰直角三角形,请说明理由.