题目内容
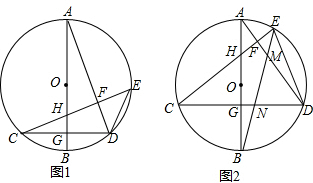
15.如图1,在⊙O中,直径AB⊥弦CD,垂足为点G,连接AD,过点C作CF⊥AD,垂足为点F,与AB相交于点H,与⊙O相交于点E,连接DE.(1)求证:∠E=2∠C;
(2)求证:DE=CH;
(3)如图2,连接BE,分别于AD、CD相交于点M、N,当OH=2OG,HF=$\sqrt{10}$时,求线段EN的长.
分析 (1)连接AC,根据垂径定理和等弧所对的圆周角相等,结合等角的余角相等即可证明结论;
(2)连接BC,运用同弧(等弧)所对的圆周角相等,结合同角的余角相等和等量代换即可证明;先证明BC=CH,再证明BC=DE;
(3)根据已知设出OG和OH,结合(2)表示BG,进而用x表示半径、直径,结合勾股定理表示CH,BE,结合△BGN∽△BEA,即可求解.
解答 解:(1)如图1,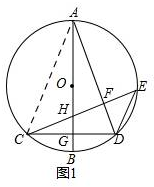
连接AC,
∵直径AB⊥弦CD,
∴弧BC=弧BD,∠CAB=∠BAD,
∴∠CAD=2∠BAD,
∴∠E=∠CAD=2∠BAD,
易证:∠C+∠CDA=90°,∠BAD+∠CDA=90°,
∴∠BAD=∠C,
∴∠E=2∠C;
(2)如图2,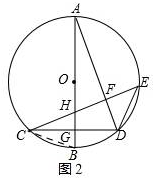
连接BC,由直径AB⊥弦CD,CF⊥AD,易证:∠CHB=∠ADC,
又∵∠ADC=∠B,
∴∠B=∠CHB,
∴CH=CB,
由(1)知∠E=2∠C,弧BC=弧BD
∴弧CD=2弧DE,
∴弧BC=弧DE,
∴BC=DE,
∴DE=CH;
(3)如图3,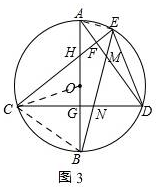
由OH=2OG,可设OG=x,则OH=2x,
于是,HG=3x,
由(2)知,BC=CH,
∵AB⊥CD,
∴BG=GH=3x,
∴OB=4x,OC=4x,AB=8x,AH=2x,
由勾股定理可求,BE=$2\sqrt{15}$x,CG=$\sqrt{15}$x,CH=$2\sqrt{6}$x,
∵弧DE=弧BD,
∴∠BAD=∠DCE,
∴sin∠BAD=sin∠DCE,
∴$\frac{HF}{AH}=\frac{HG}{CH}$,
解得:x=$\frac{2\sqrt{15}}{3}$,
∴BE=$2\sqrt{15}$x=20,
在△BGN与△BEA中,∠GBN=∠EBA,∠BGN=∠BEA=90°,
∴△BGN∽△BEA,
∴$\frac{BN}{AB}=\frac{BG}{BE}$,
∴$\frac{BN}{8x}=\frac{3x}{2\sqrt{15}x}$,
解得:BN=$\frac{24x}{2\sqrt{15}}$=8,
∴EN=BE-BN=12.
点评 此题主要考查圆的综合问题,熟悉圆的相关性质,会结合题意灵活运用勾股定理和方程思想,会借助相似三角形构建等量关系是解题的关键.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案| A. | -1 | B. | 6 | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
| A. | $y=\frac{1}{x}+1$ | B. | y=-2x | C. | y=x2+1 | D. | y=kx+1(k是常数) |
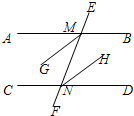 如图,AB∥CD,MG平分∠AMN,NH平分∠MND.
如图,AB∥CD,MG平分∠AMN,NH平分∠MND. 在图的方格纸中画出△ABC关于y轴对称的图形.
在图的方格纸中画出△ABC关于y轴对称的图形. 如图,皋兰山某处有一座信号塔AB,山坡BC的坡度为1:$\sqrt{3}$,现为了测量塔高AB,测量人员选择山坡C处为一测量点,测得∠DCA=45°,然后他顺山坡向上行走100米到达E处,再测得∠FEA=60°.
如图,皋兰山某处有一座信号塔AB,山坡BC的坡度为1:$\sqrt{3}$,现为了测量塔高AB,测量人员选择山坡C处为一测量点,测得∠DCA=45°,然后他顺山坡向上行走100米到达E处,再测得∠FEA=60°.