题目内容
17.在Rt△ABC中,∠BAC=90°,点D是AC上一动点,连接BD,以BD为一边作△BDE,且DB=DE.(1)如图1,当点E在BC上时,过点E作EP⊥AC,垂足为P,若∠ABD=∠PDE,则AD与PE是否相等?为什么?
(2)当点E位于图2所示位置时,连接EC,过点E向线段AC所在直线作垂线,垂足为G,若AC=AB,∠BDE=90°,则GE与CG有何数量关系?请说明理由.

分析 (1)结论:AD=PE.欲证明AD=PE,只要证明△EPD≌△DAB即可;
(2)首先证明△EDG≌△DBA,推出DG=AB,AD=GE,由AB=AC,推出DG=AC,推出AD=AC-DC=DG-DC=CG,可得GE=CG;
解答 解:(1)结论:AD=PE.
理由:如图1中,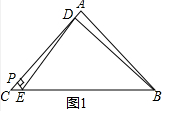
∵EP⊥AC,
∴∠EPD=∠DAB=90°,
在△EPD和△DAB中,
$\left\{\begin{array}{l}{∠PDE=∠ABD}\\{∠EPD=∠DAB}\\{ED=DB}\end{array}\right.$,
∴△EPD≌△DAB(AAS),
∴AD=PE.
(2)结论:GE=CG.
理由:如图2中,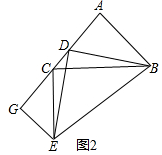
∵∠BDE=90°,
∴∠EDG+∠ADB=90°,
∵∠BAC=90°,
∴∠ADB+∠DBA=90°,
∴∠EDC=∠DBA,
在△EDG和△DBA中,
$\left\{\begin{array}{l}{∠DGE=∠BAD}\\{∠EDC=∠DBA}\\{DE=BD}\end{array}\right.$,
∴△EDG≌△DBA,
∴DG=AB,AD=GE,
∵AB=AC,
∴DG=AC,
∴AD=AC-DC=DG-DC=CG,
∴GE=CG.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
7.芯片广泛用于计算机,电脑,手机等电子产品中,其物理效应运用了数学中的二进制原理,下表为二进制和二进制的换算原理,
则二进制1001101÷1011的结果是( )
| 十进制 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| 二进制 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | … |
| A. | 1001 | B. | 111 | C. | 1101 | D. | 110 |
 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示. 如图,△ABC中,∠ACB=90°,∠CAB=45°,E是BC边上任意一点,过点C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.
如图,△ABC中,∠ACB=90°,∠CAB=45°,E是BC边上任意一点,过点C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.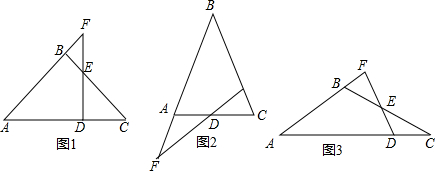
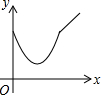
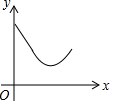
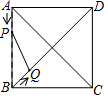 如图,正方形ABCD中,动点P的运动路线为AB→BC,动点Q的运动路线为对角线BD,点P,Q以同样的速度分别从A,B两点同时出发匀速前进,当一个点到达终点停止运动时,另一个点也随之停止.设点P的运动路程为x,PQ的长为y,则下列能大致表示y与x的函数关系的图象为( )
如图,正方形ABCD中,动点P的运动路线为AB→BC,动点Q的运动路线为对角线BD,点P,Q以同样的速度分别从A,B两点同时出发匀速前进,当一个点到达终点停止运动时,另一个点也随之停止.设点P的运动路程为x,PQ的长为y,则下列能大致表示y与x的函数关系的图象为( )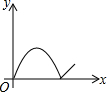

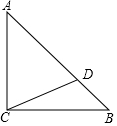 如图,在△ABC中,∠ACB=90°,AC=BC=AD
如图,在△ABC中,∠ACB=90°,AC=BC=AD