题目内容
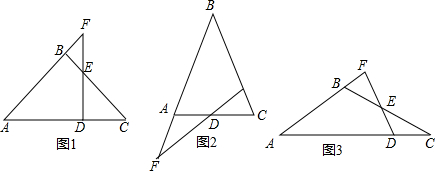
5.等腰△ABC中,AB=BC,D为底边AC上一点,E在射线CB上,∠CDE=∠ABC=α,直线DE交直线AB于F.(1)如图1,当α=90°,AB=2时,求DE+DF的值;
(2)如图2,当α=30°时,求$\frac{AF}{AD}$的值;
(3)当α=120°时,若DE+DF=3$\sqrt{3}$BF,直接写出$\frac{CE}{BC}$的值.
分析 (1)只要证明△DEC,△ADF是等腰直角三角形即可解决问题.
(2)如图2中,作AH⊥EF于H.易证∠F=45°,设AH=FH=a,则AF=$\sqrt{2}$a,AD=2a,由此即可解决问题;
(3)首先证明∠F=90°,设BF=b,则BE=2b,EF=$\sqrt{3}$b,由DE+DF=3$\sqrt{3}$BF,推出DE=$\sqrt{3}$b,作DH⊥EC于H,由∠C=∠DEC=30°,推出DE=DC,由DH⊥EC,推出EH=HC,可得EH=HC=$\frac{3}{2}$b,推出EC=3b,BC=5b,由此即可解决问题;
解答 解:(1)如图1中,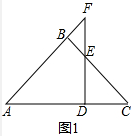
∵BC=BA,∠ABC=90°,
∴∠A=∠C=45°,
∵∠CDE=∠ABC=90°,
∴∠DEC=∠BEF=∠F=45°,
∴∠A=∠F,
∴DE=DC,DF=DA,
∴DE+DF=DC+DA=AC,
在Rt△ABC中,AC=$\sqrt{2}$AB=2$\sqrt{2}$,
∴DE+DF=2$\sqrt{2}$.
(2)如图2中,作AH⊥EF于H.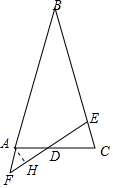
∵BA=BC,∠B=∠CDE=30°,
∴∠BAC=∠C=75°,
∴∠ADE=∠CDE=30°,∠F=45°,
∴AH=FH,设AH=FH=a,则AF=$\sqrt{2}$a,AD=2a,
∴$\frac{AF}{AD}$=$\frac{\sqrt{2}a}{2a}$=$\frac{\sqrt{2}}{2}$.
(3)如图3中,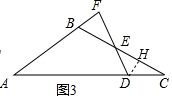
∵BA=BC,∠ABC=120°,
∴∠A=∠C=30°,
∵∠CDE=∠ABC=120°,
∴∠DEC=∠BEF=30°,
∵∠ABC=∠F+∠BEF,
∴∠F=90°,设BF=b,则BE=2b,EF=$\sqrt{3}$b,
∵DE+DF=3$\sqrt{3}$BF,
∴2DE+EF=3$\sqrt{3}$BF,
∴2DE+$\sqrt{3}$b=3$\sqrt{3}$b,
∴DE=$\sqrt{3}$b,作DH⊥EC于H,
∵∠C=∠DEC=30°,
∴DE=DC,∵DH⊥EC,
∴EH=HC,
∴EH=HC=$\frac{3}{2}$b,
∴EC=3b,BC=5b,
∴$\frac{CE}{BC}$=$\frac{3b}{5b}$=$\frac{3}{5}$.
点评 本题考查等腰三角形的性质和判定、解直角三角形、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会利用参数解决问题,属于中考压轴题.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案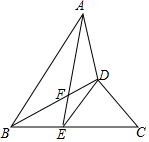 如图,线段BD平分∠ABC,且AB=BC,E是线段BC上一点,DE=DC,连接AE交BD于点F.
如图,线段BD平分∠ABC,且AB=BC,E是线段BC上一点,DE=DC,连接AE交BD于点F. 如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一直线上.
如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一直线上. 如图,在△ABC中,∠ACB=90°,AC=BC,BE是中线,CG平分∠ACB交BE于点G,F为AB边上一点,且∠ACF=∠CBG
如图,在△ABC中,∠ACB=90°,AC=BC,BE是中线,CG平分∠ACB交BE于点G,F为AB边上一点,且∠ACF=∠CBG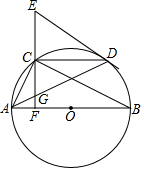 如图,在⊙O中,AB为直径,点C,D为圆上两点,连接AC,BC,过点C作AB的垂线,垂足为点F,过点D作⊙O的切线交FC的延长线于点E,连接AD交CF于点G.
如图,在⊙O中,AB为直径,点C,D为圆上两点,连接AC,BC,过点C作AB的垂线,垂足为点F,过点D作⊙O的切线交FC的延长线于点E,连接AD交CF于点G.
