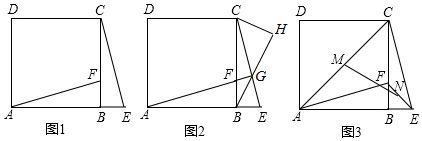
题目内容
2.某市有一块由三条公路围成的三角形绿地,现准备在其中建一亭子供人们休息,而且要使亭子中心到三条公路的距离相等,则可供选择的地方有1处.分析 由已知条件,利用角的平分线上的点到角的两边的距离相等可知在三角的平分线的交点上.
解答 解:如下图所示.
分别作三角形绿地两个角的平分线交于点P,点P即为所求.
故可供选择的地方有1处,
故答案为:1.
点评 本题主要考查角平分线上的点到角两边距离相等的性质;保留作图题的痕迹是正确解答本题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
7.由一列数按如下规律排列:-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{3}}{4}$,$\frac{1}{4}$,-$\frac{\sqrt{5}}{16}$,-$\frac{\sqrt{6}}{32}$,-$\frac{\sqrt{7}}{64}$,则第2017个数是( )
| A. | $\frac{\sqrt{2017}}{{2}^{2016}}$ | B. | -$\frac{\sqrt{2017}}{{2}^{2016}}$ | C. | $\frac{\sqrt{2018}}{{2}^{2017}}$ | D. | -$\frac{\sqrt{2018}}{{2}^{2017}}$ |
 如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一直线上.
如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一直线上.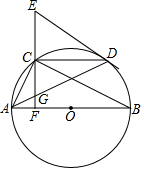 如图,在⊙O中,AB为直径,点C,D为圆上两点,连接AC,BC,过点C作AB的垂线,垂足为点F,过点D作⊙O的切线交FC的延长线于点E,连接AD交CF于点G.
如图,在⊙O中,AB为直径,点C,D为圆上两点,连接AC,BC,过点C作AB的垂线,垂足为点F,过点D作⊙O的切线交FC的延长线于点E,连接AD交CF于点G.