题目内容
17.(1)计算:$\sqrt{2}$cos45°-($\frac{1}{3}$)0(2)下面是小明化简分式的过程,请仔细阅读,并解答所提出的问题.
解:$\frac{2}{x+2}$-$\frac{x-6}{{x}^{2}-4}$=$\frac{2(x-2)}{(x+2)(x-2)}$-$\frac{x-6}{(x+2)(x-2)}$…第一步
=2(x-2)-x+6…第二步
=2x-4-x+6…第三步
=x+2…第四步
小明的做法从第二步开始出现错误,正确的化简结果是$\frac{1}{x-2}$.
分析 (1)根据0次幂,三角函数即可解答;
(2)根据分式的化简,即可解答;
解答 解:(1)原式=$\sqrt{2}×\frac{\sqrt{2}}{2}-1$
=1-1
=0.
(2)小明的做法从地二步开始出现错误;
正确化简结果是:$\frac{1}{x-2}$.
故答案为:二,$\frac{1}{x-2}$.
点评 本题考查了0次幂、三角函数值、分式的化简,解决本题的关键是明确分式的加减不要去掉分母.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.下列图形既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
5. 如图,AB∥CD,∠ABE=60°,∠D=50°,则∠E的度数为( )
如图,AB∥CD,∠ABE=60°,∠D=50°,则∠E的度数为( )
 如图,AB∥CD,∠ABE=60°,∠D=50°,则∠E的度数为( )
如图,AB∥CD,∠ABE=60°,∠D=50°,则∠E的度数为( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
9.在函数y=$\frac{{\sqrt{x+1}}}{x-2}$中,自变量x的取值范围是( )
| A. | x≤-1 | B. | x≥-1 | C. | x≤-1且x≠2 | D. | x≥-1且x≠2 |
6. 如图是一个底面半径为1,高为2的圆锥,这个圆锥的侧面积是( )
如图是一个底面半径为1,高为2的圆锥,这个圆锥的侧面积是( )
 如图是一个底面半径为1,高为2的圆锥,这个圆锥的侧面积是( )
如图是一个底面半径为1,高为2的圆锥,这个圆锥的侧面积是( )| A. | $\sqrt{3}$ | B. | $\sqrt{3}π$ | C. | $\sqrt{5}π$ | D. | $\sqrt{5}$ |
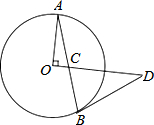 如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.
如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.