题目内容
为了迎接体育中考,某校九年级开展了体育中考项目的第一次模拟测验. 下图为某校九年级同学各项目达标人数统计图:
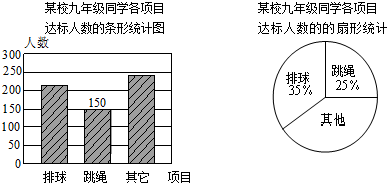
(1)在九年级学生中,达标的总人数是 ;
(2)在扇形统计图中,表示“其他”项目扇形的圆心角的度数是 ;
(3)经过一段时间的练习,在第二次模拟测验中,“排球”项目达标的人数增长到了231人,则“排球”项目达标人数的增长率是多少?

(1)在九年级学生中,达标的总人数是
(2)在扇形统计图中,表示“其他”项目扇形的圆心角的度数是
(3)经过一段时间的练习,在第二次模拟测验中,“排球”项目达标的人数增长到了231人,则“排球”项目达标人数的增长率是多少?
考点:条形统计图,扇形统计图
专题:
分析:(1)利用该班共有学生数=跳绳的人数÷它的百分比求解即可;
(2)利用“其他”项目扇形的圆心角的度数=360°×“其他”项目所对应的百分比求解即可;
(3)先求出第一次模拟测验中“排球”项目达标的人数,又已知第二次模拟测验中“排球”项目达标的人数,那么“排球”项目达标人数的增长率=(第二次模拟测验中“排球”项目达标的人数-第一次模拟测验中“排球”项目达标的人数)÷第一次模拟测验中“排球”项目达标的人数×100%.
(2)利用“其他”项目扇形的圆心角的度数=360°×“其他”项目所对应的百分比求解即可;
(3)先求出第一次模拟测验中“排球”项目达标的人数,又已知第二次模拟测验中“排球”项目达标的人数,那么“排球”项目达标人数的增长率=(第二次模拟测验中“排球”项目达标的人数-第一次模拟测验中“排球”项目达标的人数)÷第一次模拟测验中“排球”项目达标的人数×100%.
解答:
解:(1)150÷25%=600.
即在九年级学生中,达标的总人数是600;
(2)360°×(1-35%-25%)=144°.
即在扇形统计图中,表示“其他”项目扇形的圆心角的度数是144°;
(3)∵第一次模拟测验中,“排球”项目达标的人数为:600×35%=210,
又在第二次模拟测验中,“排球”项目达标的人数增长到了231人,
∴“排球”项目达标人数的增长率是:
×100%=10%.
故答案为600;144°.
即在九年级学生中,达标的总人数是600;
(2)360°×(1-35%-25%)=144°.
即在扇形统计图中,表示“其他”项目扇形的圆心角的度数是144°;
(3)∵第一次模拟测验中,“排球”项目达标的人数为:600×35%=210,
又在第二次模拟测验中,“排球”项目达标的人数增长到了231人,
∴“排球”项目达标人数的增长率是:
| 231-210 |
| 210 |
故答案为600;144°.
点评:本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
已知等腰△ABC中,AD⊥BC于点D,且AD=
BC,则△ABC底角的度数为( )
| 1 |
| 2 |
| A、45°或75° |
| B、75° |
| C、45°或75°或15° |
| D、60° |
 下面如图是以右边四个图中的哪一个绕着直线旋转一周得到的( )
下面如图是以右边四个图中的哪一个绕着直线旋转一周得到的( )A、 |
B、 |
C、 |
D、 |
 某公司为了获取一种电子产品的销售信息,对这种产品进行了试销(销售单价不高于70元,且销售单价为正整数),得到如下数据:
某公司为了获取一种电子产品的销售信息,对这种产品进行了试销(销售单价不高于70元,且销售单价为正整数),得到如下数据:
 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CE平分∠ACB,DE是AB的中垂线.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CE平分∠ACB,DE是AB的中垂线. 如图,用一个边长为6cm的等边三角形纸片制作一个最大的正六边形,则这个正六边形的边心距是
如图,用一个边长为6cm的等边三角形纸片制作一个最大的正六边形,则这个正六边形的边心距是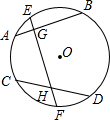 已知:如图,G、H分别是⊙O的弦AB,CD的中点,OG=OH,求证:
已知:如图,G、H分别是⊙O的弦AB,CD的中点,OG=OH,求证: