题目内容
3. 如图,已知:矩形OABC的顶点A,C分别在x,y轴的正半轴上,O为平面直角坐标系的原点;直线y=x+1分别交x,y轴及矩形OABC的BC边于E,M,F,且△EOM≌△FCM;过点F的双曲线y=$\frac{k}{x}$(x>0)与AB交于点N.
如图,已知:矩形OABC的顶点A,C分别在x,y轴的正半轴上,O为平面直角坐标系的原点;直线y=x+1分别交x,y轴及矩形OABC的BC边于E,M,F,且△EOM≌△FCM;过点F的双曲线y=$\frac{k}{x}$(x>0)与AB交于点N.(1)求k的值;
(2)当x0<x<1时,$\frac{k}{x}$>x+1;
(3)若F为BC中点,求BN的长.
分析 (1)先根据一次函数的解析式求出E、M两点的坐标,再由△EOM≌△FCM得出OM=OC=1,故可得出F点的坐标,根据点F在双曲线上即可得出k的值;
(2)利用函数图象即可直接得出结论;
(3)先求出N点坐标,再由矩形的性质即可得出结论.
解答 解:∵当x=0时,y=1;当y=0时,x=-1
∴OE=OM=1.
∵△EOM≌△FCM,
∴CM=CF=OE=OM=1,
∴F(1,2).
(1)∵y=$\frac{k}{x}$的图象过点F(1,2),
∴k=1×2=2;
(2)由函数图象可知,当0<x<1时,$\frac{k}{x}$>x+1.
故答案为:0<x<1;
(3)∵F为矩形OABC的BC边中点,
∴B(2,2)
∴N(2,a)
∵N在y=$\frac{2}{x}$上
∴a=$\frac{2}{2}$,
∴a=1,
∴AN=1.
∵AB=OC=2,
∴BN=BA-AN=2-1=1.
点评 本题考查的是反比例函数综合题,涉及到反比例函数图象上点的坐标特点、矩形的性质等知识,在解答此题时要注意数形结合思想的灵活运用.

练习册系列答案
相关题目
8.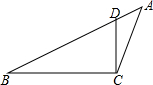 如图,在△ABC中,点D在AB上,在下列四个条件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=AD•AB;④AB•CD=AD•CB,能满足△ADC与△ACB相似的条件是( )
如图,在△ABC中,点D在AB上,在下列四个条件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=AD•AB;④AB•CD=AD•CB,能满足△ADC与△ACB相似的条件是( )
 如图,在△ABC中,点D在AB上,在下列四个条件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=AD•AB;④AB•CD=AD•CB,能满足△ADC与△ACB相似的条件是( )
如图,在△ABC中,点D在AB上,在下列四个条件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=AD•AB;④AB•CD=AD•CB,能满足△ADC与△ACB相似的条件是( )| A. | ①、②、③ | B. | ①、③、④ | C. | ②、③、④ | D. | ①、②、④ |
12.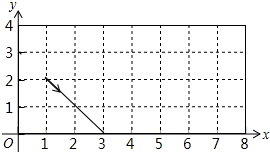 如图,动点P从(1,2)出发,沿图中箭头所示方向运动,每当碰到长方形的边时反弹(反弹时反射角等于入射角),假设反弹可以无限进行下去,则在点P运动路径上的点是( )
如图,动点P从(1,2)出发,沿图中箭头所示方向运动,每当碰到长方形的边时反弹(反弹时反射角等于入射角),假设反弹可以无限进行下去,则在点P运动路径上的点是( )
 如图,动点P从(1,2)出发,沿图中箭头所示方向运动,每当碰到长方形的边时反弹(反弹时反射角等于入射角),假设反弹可以无限进行下去,则在点P运动路径上的点是( )
如图,动点P从(1,2)出发,沿图中箭头所示方向运动,每当碰到长方形的边时反弹(反弹时反射角等于入射角),假设反弹可以无限进行下去,则在点P运动路径上的点是( )| A. | (0,5) | B. | (5,0) | C. | (3,3) | D. | (7,3) |
 如图,在等边△ABC中,AD⊥BC于D,若AB=4cm,AD=2$\sqrt{3}$cm,E为AB的中点,P为AD上一点,PE+PB的最小值为2$\sqrt{3}$.
如图,在等边△ABC中,AD⊥BC于D,若AB=4cm,AD=2$\sqrt{3}$cm,E为AB的中点,P为AD上一点,PE+PB的最小值为2$\sqrt{3}$.