题目内容
11.将进货单价为40元的商品按50元售出,能卖出500个,已知这种商品每涨1元其销量就减少10个,若想获得8000元利润,售价应为多少?分析 总利润=销售量×每个利润.设涨价x元能赚得8000元的利润,即售价定为每个(x+50)元,应进货(500-10x)个,根据为了赚得8000元的利润,可列方程求解.
解答 解:设涨价x元能赚得8000元的利润,即售价定为每个(x+50)元,应进货(500-10x)个,
依题意得:(50-40+x)(500-10x)=8000,
解得x1=10,x2=30,
当x=10时,x+50=60;
当x=30时,x+50=80.
答:售价定为每个60元或每个80元能获得获得8000元利润.
点评 本题考查一元二次方程的应用,关键看到涨价和销售量的关系,然后以利润做为等量关系列方程求解.

练习册系列答案
相关题目
6.y=$\frac{6}{x}$上有两点A(x1,y1)与B(x2,y2),若x1<x2,则y1与y2的关系是( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能确定 |
16.tan30°=( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
1.若|m+3|+(n-2)2=0,则m+n的值为( )
| A. | 1 | B. | -1 | C. | 5 | D. | -5 |
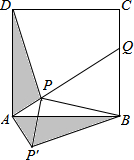 如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q. 如图,已知:矩形OABC的顶点A,C分别在x,y轴的正半轴上,O为平面直角坐标系的原点;直线y=x+1分别交x,y轴及矩形OABC的BC边于E,M,F,且△EOM≌△FCM;过点F的双曲线y=$\frac{k}{x}$(x>0)与AB交于点N.
如图,已知:矩形OABC的顶点A,C分别在x,y轴的正半轴上,O为平面直角坐标系的原点;直线y=x+1分别交x,y轴及矩形OABC的BC边于E,M,F,且△EOM≌△FCM;过点F的双曲线y=$\frac{k}{x}$(x>0)与AB交于点N.