题目内容
8.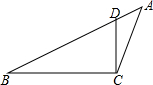 如图,在△ABC中,点D在AB上,在下列四个条件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=AD•AB;④AB•CD=AD•CB,能满足△ADC与△ACB相似的条件是( )
如图,在△ABC中,点D在AB上,在下列四个条件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=AD•AB;④AB•CD=AD•CB,能满足△ADC与△ACB相似的条件是( )| A. | ①、②、③ | B. | ①、③、④ | C. | ②、③、④ | D. | ①、②、④ |
分析 由∠A是公共角,根据有两组角对应相等的两个三角形相似与两组对应边的比相等且夹角对应相等的两个三角形相似,判定△ABC与△ACD相似,即可得出结果.
解答 解:∵∠A是公共角,
∴当∠ACD=∠B时,△ADC∽△ACB(有两组角对应相等的两个三角形相似);
当∠ADC=∠ACB时,△ADC∽△ACB(有两组角对应相等的两个三角形相似);
当AC2=AD•AB时,即$\frac{AC}{AB}=\frac{AD}{AC}$,△ADC∽△ACB(两组对应边的比相等且夹角对应相等的两个三角形相似).
当AB•CD=AD•CB,即$\frac{CD}{AD}=\frac{CB}{AB}$时,∠A不是夹角,则不能判定△ADC与△ACB相似;
∴能够判定△ABC与△ACD相似的条件是:①②③.
故选A.
点评 此题考查了相似三角形的判定.此题难度不大,熟记相似三角形的判定方法是解决问题的关键.

练习册系列答案
相关题目
18.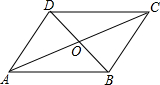 如图,?ABCD对角线AC与BD相交于点O,如果$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AD}$=$\overrightarrow{n}$,那么下列选项中,与向量$\frac{1}{2}$($\overrightarrow{m}$+$\overrightarrow{n}$)相等的向量是( )
如图,?ABCD对角线AC与BD相交于点O,如果$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AD}$=$\overrightarrow{n}$,那么下列选项中,与向量$\frac{1}{2}$($\overrightarrow{m}$+$\overrightarrow{n}$)相等的向量是( )
 如图,?ABCD对角线AC与BD相交于点O,如果$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AD}$=$\overrightarrow{n}$,那么下列选项中,与向量$\frac{1}{2}$($\overrightarrow{m}$+$\overrightarrow{n}$)相等的向量是( )
如图,?ABCD对角线AC与BD相交于点O,如果$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AD}$=$\overrightarrow{n}$,那么下列选项中,与向量$\frac{1}{2}$($\overrightarrow{m}$+$\overrightarrow{n}$)相等的向量是( )| A. | $\overrightarrow{OA}$ | B. | $\overrightarrow{OB}$ | C. | $\overrightarrow{OC}$ | D. | $\overrightarrow{OD}$ |
16.tan30°=( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
17.若一元二次方程(1-2k)x2+8x-6=0没有实数根,那么k的最小值是( )
| A. | 2 | B. | 0 | C. | 1 | D. | 3 |
 如图,已知:矩形OABC的顶点A,C分别在x,y轴的正半轴上,O为平面直角坐标系的原点;直线y=x+1分别交x,y轴及矩形OABC的BC边于E,M,F,且△EOM≌△FCM;过点F的双曲线y=$\frac{k}{x}$(x>0)与AB交于点N.
如图,已知:矩形OABC的顶点A,C分别在x,y轴的正半轴上,O为平面直角坐标系的原点;直线y=x+1分别交x,y轴及矩形OABC的BC边于E,M,F,且△EOM≌△FCM;过点F的双曲线y=$\frac{k}{x}$(x>0)与AB交于点N.