题目内容
【问题情景】
我们知道,多边形的一边与它的邻边的延长线组成的角,叫做多边形的外角.
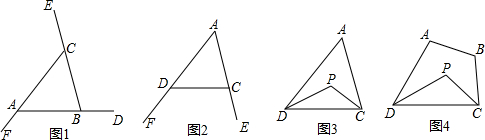
如图1所示,∠CBD、∠BAF、∠ACE是△ABC的三个外角,下面我们来探究∠CBD、∠BAF、∠ACE和△ABC三内角之间的数量关系.
【方法感悟】
解:因为在△ABC中,
∠ABC+∠BAC+∠ACB=180°,
所以∠BAC+∠ACB=180°-∠ABC.
因为∠ABC+∠CBD=180°,
所以∠CBD=180°-∠ABC.
所以∠CBD=∠BAC+∠ACB.
同理可得:∠BAF=∠ABC+∠ACB,∠ACE=∠BAC+∠ABC.
因此,我们得到一个重要的结论:三角形的一个外角等于与它不相邻的两个内角的和.
【解决问题】
问题一:
已知:如图2,∠FDC与∠ECD分别为△ADC的两个外角,请直接利用上述结论,试探究∠FDC+∠ECD与∠A的数量关系.
问题二:
已知:如图3,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
问题三:
已知:如图4,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论直接写出∠P与∠A+∠B的数量关系. .
我们知道,多边形的一边与它的邻边的延长线组成的角,叫做多边形的外角.
如图1所示,∠CBD、∠BAF、∠ACE是△ABC的三个外角,下面我们来探究∠CBD、∠BAF、∠ACE和△ABC三内角之间的数量关系.

【方法感悟】
解:因为在△ABC中,
∠ABC+∠BAC+∠ACB=180°,
所以∠BAC+∠ACB=180°-∠ABC.
因为∠ABC+∠CBD=180°,
所以∠CBD=180°-∠ABC.
所以∠CBD=∠BAC+∠ACB.
同理可得:∠BAF=∠ABC+∠ACB,∠ACE=∠BAC+∠ABC.
因此,我们得到一个重要的结论:三角形的一个外角等于与它不相邻的两个内角的和.
【解决问题】
问题一:
已知:如图2,∠FDC与∠ECD分别为△ADC的两个外角,请直接利用上述结论,试探究∠FDC+∠ECD与∠A的数量关系.
问题二:
已知:如图3,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
问题三:
已知:如图4,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论直接写出∠P与∠A+∠B的数量关系.
考点:多边形内角与外角,三角形内角和定理,三角形的外角性质
专题:探究型
分析:(1)根据三角形的一个外角等于与它不相邻的两个内角的和,可得∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,再根据三角形内角和公式即可求解;
(2)根据角平分线的定义和三角形内角和定理可得∠P与∠A的数量关系;
(3)根据角平分线的定义和四边形内角和定理可得∠P与∠A+∠B的数量关系.
(2)根据角平分线的定义和三角形内角和定理可得∠P与∠A的数量关系;
(3)根据角平分线的定义和四边形内角和定理可得∠P与∠A+∠B的数量关系.
解答:解:(1)∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,
∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A.
(2)∵DP平分∠ADC,
∴∠PDC=
∠ADC.
同理,∠PCD=
∠ACD.
∴∠DPC=180°-∠PDC-∠PCD=180°-
(180°-∠A)=90°+
∠A;
(3)∵DP平分∠ADC,
∴∠PDC=
∠ADC.
同理,∠PCD=
∠BCD.
∴∠P=180°-∠PDC-∠PCD=180°-
(360°-∠A-∠B)=
(∠A+∠B).
故答案为:∠P=
(∠A+∠B).
∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A.
(2)∵DP平分∠ADC,
∴∠PDC=
| 1 |
| 2 |
同理,∠PCD=
| 1 |
| 2 |
∴∠DPC=180°-∠PDC-∠PCD=180°-
| 1 |
| 2 |
| 1 |
| 2 |
(3)∵DP平分∠ADC,
∴∠PDC=
| 1 |
| 2 |
同理,∠PCD=
| 1 |
| 2 |
∴∠P=180°-∠PDC-∠PCD=180°-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:∠P=
| 1 |
| 2 |
点评:本题考查了三角形的外角性质,角平分线的定义,三角形的内角和定理,多边形的内角和公式,此类题目根据同一个解答思路求解是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,关于线段、射线和直线的条数,下列说法正确的是( )
如图所示,关于线段、射线和直线的条数,下列说法正确的是( )| A、五条线段,三条射线 |
| B、一条直线,三条线段 |
| C、三条线段,两条射线,一条直线 |
| D、三条线段,三条射线 |
一条弦所对的圆心角是60°,则它所对的圆周角是( )
| A、30° |
| B、150° |
| C、30°或150° |
| D、60°或120° |
图中,∠1与∠2是对顶角的是( )
A、 |
B、 |
C、 |
D、 |
 如图,把一个圆分成4个扇形,其中∠AOD=∠BOD=90°,∠AOC=3∠BOC,这四个扇形的面积比是( )
如图,把一个圆分成4个扇形,其中∠AOD=∠BOD=90°,∠AOC=3∠BOC,这四个扇形的面积比是( )| A、1:2:2:3 |
| B、3:2:2:3 |
| C、1:2:2:1 |
| D、4:2:2:3 |
 如图,在△ABC中,AC=BC,AD平分∠BAC,∠ADC=60°,求∠C的度数.
如图,在△ABC中,AC=BC,AD平分∠BAC,∠ADC=60°,求∠C的度数. 如图,△ABC中,∠BAC=120°,∠B=30°,AD⊥AB,垂足为A,CD=2cm.求AB的长及△ABC的面积.
如图,△ABC中,∠BAC=120°,∠B=30°,AD⊥AB,垂足为A,CD=2cm.求AB的长及△ABC的面积. 实验发现:光线从空气射入玻璃中,会发生折射现象,光线从玻璃射入空气中,同样也会发生折射现象.如图,光线从空气中射入玻璃中再从玻璃射入空气中,已知∠1=∠2,∠3=∠4,那么光线AB与CD是否平行?说明理由.
实验发现:光线从空气射入玻璃中,会发生折射现象,光线从玻璃射入空气中,同样也会发生折射现象.如图,光线从空气中射入玻璃中再从玻璃射入空气中,已知∠1=∠2,∠3=∠4,那么光线AB与CD是否平行?说明理由.