题目内容
 如图,△ABC中,∠BAC=120°,∠B=30°,AD⊥AB,垂足为A,CD=2cm.求AB的长及△ABC的面积.
如图,△ABC中,∠BAC=120°,∠B=30°,AD⊥AB,垂足为A,CD=2cm.求AB的长及△ABC的面积.考点:含30度角的直角三角形
专题:
分析:根据三角形内角和定理,由∠BAC=120°,∠B=30°,AD⊥AB求得∠DAC=∠C=30°,由此证得△ADC是等腰三角形,即可求出AD的长,解Rt△ABD,得出BD、AB的长,求出BC=BD+CD,再作AE⊥BC于E.在Rt△ABE中,根据含30度角的直角三角形的性质得出AE=
AB=
cm,然后利用△ABC的面积=
BC•AE,代入数据计算即可.
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
解答: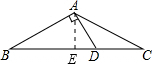 解:∵在△ABC中,∠BAC=120°,∠B=30°,AD⊥AB,
解:∵在△ABC中,∠BAC=120°,∠B=30°,AD⊥AB,
∴∠C=180°-120°-30°=30°,∠DAC=120°-90°=30°;
∴∠DAC=∠C=30°,
∴CD=AD=2cm.
在Rt△ABD中,∵∠BAD=90°,∠B=30°,
∴BD=2AD=4cm,AB=
=2
cm,
∴BC=BD+CD=6cm.
作AE⊥BC于E.
在Rt△ABE中,∵∠BEA=90°,∠B=30°,
∴AE=
AB=
cm,
∴△ABC的面积=
BC•AE=
×6×
=3
(cm2).
 解:∵在△ABC中,∠BAC=120°,∠B=30°,AD⊥AB,
解:∵在△ABC中,∠BAC=120°,∠B=30°,AD⊥AB,∴∠C=180°-120°-30°=30°,∠DAC=120°-90°=30°;
∴∠DAC=∠C=30°,
∴CD=AD=2cm.
在Rt△ABD中,∵∠BAD=90°,∠B=30°,
∴BD=2AD=4cm,AB=
| AD |
| tan30° |
| 3 |
∴BC=BD+CD=6cm.
作AE⊥BC于E.
在Rt△ABE中,∵∠BEA=90°,∠B=30°,
∴AE=
| 1 |
| 2 |
| 3 |
∴△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:此题主要考查含30度角的直角三角形的性质,等腰三角形的判定和性质,三角形内角和定理,三角形的面积;求得∠DAC=30°是正确解答本题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
下列几种说法中,正确的是( )
| A、0是最小的数 |
| B、数轴上距原点3个单位的点表示的数是±3 |
| C、最大的负有理数是-1 |
| D、任何有理数的绝对值都是正数 |
已知a=2,b=3,c=4,d=6,则下列各式中正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,从正面、左面、上面三个不同的方向看某个几何体得到如下的平面图形,那么这个几何体是( )
如图,从正面、左面、上面三个不同的方向看某个几何体得到如下的平面图形,那么这个几何体是( )| A、三棱柱 | B、三棱锥 |
| C、圆锥 | D、.四棱锥 |
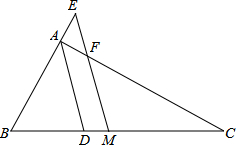 如图,△ABC中∠A的平分线为AD,M为BC的中点,过点M作ME∥AD交BA的延长线于E,交AC于F.
如图,△ABC中∠A的平分线为AD,M为BC的中点,过点M作ME∥AD交BA的延长线于E,交AC于F.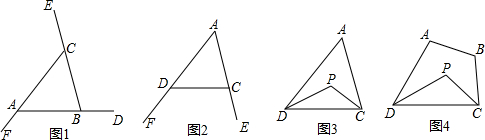

 如图,∵∠B=∠
如图,∵∠B=∠