题目内容
 实验发现:光线从空气射入玻璃中,会发生折射现象,光线从玻璃射入空气中,同样也会发生折射现象.如图,光线从空气中射入玻璃中再从玻璃射入空气中,已知∠1=∠2,∠3=∠4,那么光线AB与CD是否平行?说明理由.
实验发现:光线从空气射入玻璃中,会发生折射现象,光线从玻璃射入空气中,同样也会发生折射现象.如图,光线从空气中射入玻璃中再从玻璃射入空气中,已知∠1=∠2,∠3=∠4,那么光线AB与CD是否平行?说明理由.考点:平行线的判定
专题:应用题
分析:由∠3=∠4,可得∠5=∠6,结合条件可得∠ABC=∠BCD,可得AB∥CD.
解答:解:平行,理由如下:
∵∠3=∠4,
∴∠5=∠6,
又∵∠1=∠2,
∴∠1+∠5=∠2+∠6,
即∠ABC=∠BCD,
∴AB∥CD.
∵∠3=∠4,
∴∠5=∠6,
又∵∠1=∠2,
∴∠1+∠5=∠2+∠6,
即∠ABC=∠BCD,
∴AB∥CD.
点评:本题主要考查平行线判定,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c?a∥c.

练习册系列答案
相关题目
 如图,从正面、左面、上面三个不同的方向看某个几何体得到如下的平面图形,那么这个几何体是( )
如图,从正面、左面、上面三个不同的方向看某个几何体得到如下的平面图形,那么这个几何体是( )| A、三棱柱 | B、三棱锥 |
| C、圆锥 | D、.四棱锥 |
下列各式中从左到右的变形,是因式分解的是( )
| A、(a+3)(a-3)=a2-9 | ||
| B、x2+x-5=(x-2)(x+3)+1 | ||
C、x2+1=x(x+
| ||
| D、a2b+ab2=ab(a+b) |
 如图,在△ABC中,∠A=40°,∠ABC=80°,BD平分∠ABC,则∠BDC的度数是( )
如图,在△ABC中,∠A=40°,∠ABC=80°,BD平分∠ABC,则∠BDC的度数是( )| A、85° | B、80° |
| C、75° | D、70° |

 如图,∵∠B=∠
如图,∵∠B=∠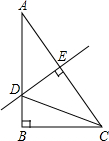 如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E式垂足,连接CD,若BD=1,则AD的长是( )
如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E式垂足,连接CD,若BD=1,则AD的长是( )