题目内容
 如图,把一个圆分成4个扇形,其中∠AOD=∠BOD=90°,∠AOC=3∠BOC,这四个扇形的面积比是( )
如图,把一个圆分成4个扇形,其中∠AOD=∠BOD=90°,∠AOC=3∠BOC,这四个扇形的面积比是( )| A、1:2:2:3 |
| B、3:2:2:3 |
| C、1:2:2:1 |
| D、4:2:2:3 |
考点:认识平面图形
专题:
分析:先求出扇形的圆心角,再利用扇形的面积公式相比求解即可.
解答:解:∵∠AOC=3∠BOC,
∴∠AOC=135°,∠BOC=45°,
∵S扇形=
πr2,
∴S扇形BOC:S扇形BOD:S扇形AOD:S扇形AOC=45:90:90:135=1:2:2:3.
故选:A.
∴∠AOC=135°,∠BOC=45°,
∵S扇形=
| n |
| 360 |
∴S扇形BOC:S扇形BOD:S扇形AOD:S扇形AOC=45:90:90:135=1:2:2:3.
故选:A.
点评:本题主要考查了扇形的面积,解题的关键是熟记扇形面积公式.

练习册系列答案
相关题目
一个正方形的面积为17,估计它的边长大小为( )
| A、2与3之间 |
| B、3与4之间 |
| C、4与5之间 |
| D、5与6之间 |
下列几种说法中,正确的是( )
| A、0是最小的数 |
| B、数轴上距原点3个单位的点表示的数是±3 |
| C、最大的负有理数是-1 |
| D、任何有理数的绝对值都是正数 |
 如图,从正面、左面、上面三个不同的方向看某个几何体得到如下的平面图形,那么这个几何体是( )
如图,从正面、左面、上面三个不同的方向看某个几何体得到如下的平面图形,那么这个几何体是( )| A、三棱柱 | B、三棱锥 |
| C、圆锥 | D、.四棱锥 |
 如图,在△ABC中,∠A=40°,∠ABC=80°,BD平分∠ABC,则∠BDC的度数是( )
如图,在△ABC中,∠A=40°,∠ABC=80°,BD平分∠ABC,则∠BDC的度数是( )| A、85° | B、80° |
| C、75° | D、70° |
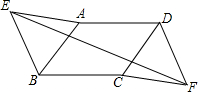 如图,在?ABCD中,以AB,DC为边在两侧作等边△AEB和等边△CFD,求证:四边形EBFD是平行四边形.
如图,在?ABCD中,以AB,DC为边在两侧作等边△AEB和等边△CFD,求证:四边形EBFD是平行四边形. 图中∠B的同旁内角有几个?分别是由哪两条直线被哪一条直线所截而成的?
图中∠B的同旁内角有几个?分别是由哪两条直线被哪一条直线所截而成的?