题目内容
某商品的进价为每件40元,售价为每件50元,每个月可卖出210件,如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元),设每件商品约售价上涨x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围.
(2)若每个月的利润为2200元,求每件商品的售价应定为多少元?
(3)每件商品的售价定为多少元时,每个月可获得最大利润?最大利润是多少元?
(1)求y与x的函数关系式,并直接写出自变量x的取值范围.
(2)若每个月的利润为2200元,求每件商品的售价应定为多少元?
(3)每件商品的售价定为多少元时,每个月可获得最大利润?最大利润是多少元?
考点:二次函数的应用
专题:
分析:(1)根据进价为每件40元,售价为每件50元,每个月可卖出210件,再根据每件商品的售价每上涨1元,则每个月少卖10件和销售利润=件数×每件的利润列出关系式,即可得出答案.
(2)每个月的利润为卖出的商品数和每件商品的乘积,即(210-x)(10+x),当每个月的利润恰为2200元时得到方程(210-x)(10+x)=2200.求此方程中x的值;
(3)根据(1)得出的函数关系式,再进行配方得出y=-10(x-5.5)2+2402.5,当x=5.5时y有最大值,从而得出答案.
(2)每个月的利润为卖出的商品数和每件商品的乘积,即(210-x)(10+x),当每个月的利润恰为2200元时得到方程(210-x)(10+x)=2200.求此方程中x的值;
(3)根据(1)得出的函数关系式,再进行配方得出y=-10(x-5.5)2+2402.5,当x=5.5时y有最大值,从而得出答案.
解答:解:(1)由题意得:y=(210-10x)(50+x-40)
=-10x2+110x+2100(0<x≤15且x为整数);
(2)根据题意,得(210-10x)(10+x)=2200.
整理,得x2-11x+10=0,解这个方程,得x1=1,x2=10
∴当x=1时,50+x=51,当x=10时,50+x=60.
答:当每件商品的售价定为51元或60元时,每个月的利润恰为2200元.
(3)根据(1)得:
y=-10x2+110x+2100,
y=-10(x-5.5)2+2402.5,
∵a=-10<0,
∴当x=5.5时,y有最大值2402.5.
∵0<x≤15,且x为整数,
当x=5时,50+x=55,y=2400(元),
当x=6时,50+x=56,y=2400(元)
∴当售价定为每件55或56元,每个月的利润最大,最大的月利润是2400元.
=-10x2+110x+2100(0<x≤15且x为整数);
(2)根据题意,得(210-10x)(10+x)=2200.
整理,得x2-11x+10=0,解这个方程,得x1=1,x2=10
∴当x=1时,50+x=51,当x=10时,50+x=60.
答:当每件商品的售价定为51元或60元时,每个月的利润恰为2200元.
(3)根据(1)得:
y=-10x2+110x+2100,
y=-10(x-5.5)2+2402.5,
∵a=-10<0,
∴当x=5.5时,y有最大值2402.5.
∵0<x≤15,且x为整数,
当x=5时,50+x=55,y=2400(元),
当x=6时,50+x=56,y=2400(元)
∴当售价定为每件55或56元,每个月的利润最大,最大的月利润是2400元.
点评:本题考查二次函数的实际应用,关键是读懂题意,找出之间的等量关系,根据每天的利润=一件的利润×销售件数,建立函数关系式,此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
相关题目
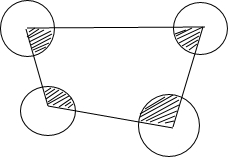 如图所示,分别以四边形的各个顶点为圆心,半径为10作圆(这些圆互不相交).问这些圆与四边形的公共部分(即图中阴影部分)的面积是多少?为什么?
如图所示,分别以四边形的各个顶点为圆心,半径为10作圆(这些圆互不相交).问这些圆与四边形的公共部分(即图中阴影部分)的面积是多少?为什么?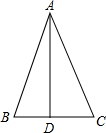 如图,在△ABC中,AB=AC,AD是BC边上的高,∠C=63°,BC=4,求∠BAD的度数及DC的长.
如图,在△ABC中,AB=AC,AD是BC边上的高,∠C=63°,BC=4,求∠BAD的度数及DC的长.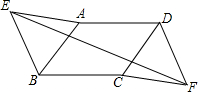 如图,在?ABCD中,以AB,DC为边在两侧作等边△AEB和等边△CFD,求证:四边形EBFD是平行四边形.
如图,在?ABCD中,以AB,DC为边在两侧作等边△AEB和等边△CFD,求证:四边形EBFD是平行四边形.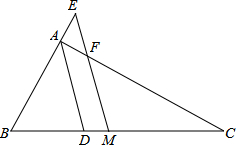 如图,△ABC中∠A的平分线为AD,M为BC的中点,过点M作ME∥AD交BA的延长线于E,交AC于F.
如图,△ABC中∠A的平分线为AD,M为BC的中点,过点M作ME∥AD交BA的延长线于E,交AC于F.