题目内容
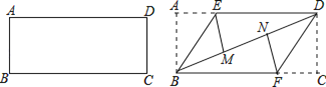
准备一张矩形纸片，按如图操作：将△ABE沿BE翻折，使点A落在对角线BD上的M点，将△CDF沿DF翻折，使点C落在对角线BD上的N点．
（1）求证：四边形BFDE是平行四边形.
（2）若四边形BFDE是菱形，BE =2，求菱形BFDE的面积．
练习册系列答案
相关题目
题目内容
准备一张矩形纸片，按如图操作：将△ABE沿BE翻折，使点A落在对角线BD上的M点，将△CDF沿DF翻折，使点C落在对角线BD上的N点．
（1）求证：四边形BFDE是平行四边形.
（2）若四边形BFDE是菱形，BE =2，求菱形BFDE的面积．
是函数
与
的一个交点，则
的值为______．
是
的直径，CD与
相切于C， 
.
的平分线.
的半径OA=6，求CE的长.
，推出
，由
，推出
，可得
.（2）在
中，求出OD，由
，可得
，由此即可解决问题.
，
，
，
，
，
是
的平分线.
的切线，
，即在
中，DC=8，OC=OA=6,所以
，
，
，
，