题目内容
2.一个不透明的袋中装有5个黄球、15个黑球和22个红球,它们出颜色外都相同.(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,使从袋中摸出一个球是黄球的概率是$\frac{1}{3}$,问取出了多少个黑球?
分析 (1)利用概率公式直接计算;
(2)设取出了x个黑球,利用概率公式得到$\frac{5+x}{42}$=$\frac{1}{3}$,然后解关于x的方程就尅.
解答 解:(1)从袋中摸出一个球是黄球的概率=$\frac{5}{5+15+22}$=$\frac{5}{42}$;
(2)设取出了x个黑球,
根据题意得$\frac{5+x}{42}$=$\frac{1}{3}$,解得x=9,
答:取出了9个黑球.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.解决本题的关键是接着概率公式.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
12.数轴上一点A表示的有理数为-2,若将A点向右平移3个单位长度后,A点表示的有理数应为( )
| A. | 3 | B. | -1 | C. | 1 | D. | -5 |
17. 如图,长方形ABCD,点B表示的数为-2,点C在原点,CD=1,以点C为圆心,CA为半径画弧,交数轴于点P,则点P表示的实数是( )
如图,长方形ABCD,点B表示的数为-2,点C在原点,CD=1,以点C为圆心,CA为半径画弧,交数轴于点P,则点P表示的实数是( )
 如图,长方形ABCD,点B表示的数为-2,点C在原点,CD=1,以点C为圆心,CA为半径画弧,交数轴于点P,则点P表示的实数是( )
如图,长方形ABCD,点B表示的数为-2,点C在原点,CD=1,以点C为圆心,CA为半径画弧,交数轴于点P,则点P表示的实数是( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | -$\sqrt{5}$ | D. | -$\sqrt{3}$ |
11. 如图,直线AB、CD相交于E,EF平分∠BED,已知∠DEF=70°,则∠AED的度数是( )
如图,直线AB、CD相交于E,EF平分∠BED,已知∠DEF=70°,则∠AED的度数是( )
 如图,直线AB、CD相交于E,EF平分∠BED,已知∠DEF=70°,则∠AED的度数是( )
如图,直线AB、CD相交于E,EF平分∠BED,已知∠DEF=70°,则∠AED的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
12.比较2100与375的大小:因为2100=(24)25=1625,375=(33)25=2725,而16<27,所以1625<2725,即2100<375.据此可知355、444、533的大小关系是( )
| A. | 355<444<533 | B. | 533<444<355 | C. | 444<533<355 | D. | 533<355<444 |
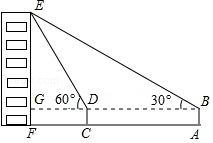 如图,小华在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进30米到达C处,又测得顶部E的仰角为60°,求大楼EF的高度.(结果精确到0.1米,参考数据$\sqrt{3}$=1.732)
如图,小华在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进30米到达C处,又测得顶部E的仰角为60°,求大楼EF的高度.(结果精确到0.1米,参考数据$\sqrt{3}$=1.732)