题目内容
17．
如图，长方形ABCD，点B表示的数为-2，点C在原点，CD=1，以点C为圆心，CA为半径画弧，交数轴于点P，则点P表示的实数是（ ）| A． | $\sqrt{3}$ | B． | $\sqrt{5}$ | C． | -$\sqrt{5}$ | D． | -$\sqrt{3}$ |
分析 利用勾股定理列式求出AC，然后根据数轴写出点P所表示的数即可．
解答 解：∵长方形ABCD的长BC为2，宽CD为1，
∴由勾股定理得，AC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，
∴PC=AC=$\sqrt{5}$，
∴点P表示的数是-$\sqrt{5}$．
故选C．
点评 本题考查了勾股定理，实数与数轴，主要是无理数在数轴上的表示，熟记定理是解题的关键．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
7．在数3、-2、0、-$\frac{5}{2}$中，最小的数是（ ）
| A． | 3 | B． | -2 | C． | 0 | D． | -$\frac{5}{2}$ |
8．
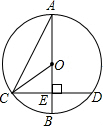如图，在⊙O中，直径AB与弦CD垂直相交于点E，连结AC，OC，若∠A=30°，OC=4，则弦CD的长是（ ）
如图，在⊙O中，直径AB与弦CD垂直相交于点E，连结AC，OC，若∠A=30°，OC=4，则弦CD的长是（ ）| A． | $2\sqrt{3}$ | B． | 4 | C． | $4\sqrt{3}$ | D． | 8 |
在矩形ABCD中，AD=4，对角线AC与BD相交于点O，过点A作AE⊥BD，垂足为E，EB=$\frac{1}{2}$OB，求AE的长．
6．下列说法中正确的是（ ）
| A． | 两条射线组成的图形叫做角 | |
| B． | 小于平角的角可分为锐角和钝角两类 | |
| C． | 射线就是直线 | |
| D． | 两点之间的所有连线中，线段最短 |
7．下列说法中不正确的是（ ）
| A． | 有理数都可以用数轴上的点来表示 | B． | 数轴上的点都表示有理数 | ||
| C． | 实数都可以用数轴上的点来表示 | D． | 数轴上的点都表示实数 |