题目内容
若关于x的一元二次方程ax2-2x+1=0有两个实数根,则实数a的取值范围是( )
| A、a≤1且a≠0 |
| B、a<1且a≠0 |
| C、a≤1 |
| D、a<1 |
考点:根的判别式
专题:
分析:由关于x的一元二次方程ax2-2x+1=0有两个实数根及一元二次方程的定义,即可得判别式△≥0,a≠0,继而可求得a的范围.
解答:解:∵关于x的一元二次方程ax2-2x+1=0有两个实数根,
∴△=b2-4ac=(-2)2-4×a×1=4-4a≥0,
解得:a≤1,
∵方程ax2-2x+6=0是一元二次方程,
∴a≠0,
∴a的范围是:a≤1且a≠0.
故选:A.
∴△=b2-4ac=(-2)2-4×a×1=4-4a≥0,
解得:a≤1,
∵方程ax2-2x+6=0是一元二次方程,
∴a≠0,
∴a的范围是:a≤1且a≠0.
故选:A.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
关于x的方程mx2-3x+2=x2是一元二次方程,则( )
| A、m>1 | B、m≠1 |
| C、m=1 | D、m≥1 |
将方程
-
=1去分母,得到6x-3-2x-2=6,错在( )
| 2x-1 |
| 2 |
| x-1 |
| 3 |
| A、最简公分母找错 |
| B、去分母时,漏乘3项 |
| C、去分母时,分子部分没有加括号 |
| D、去分母时,各项所乘的数不同 |
下列计算正确的是( )
| A、-(-4)2=16 | ||||
| B、(-42)=16 | ||||
C、(-
| ||||
| D、(2×3)2=36 |
 如图,在?ABCD中,AB=3,AD=4,E是CD的中点,则EO等于( )
如图,在?ABCD中,AB=3,AD=4,E是CD的中点,则EO等于( )| A、3 | B、4 | C、1.5 | D、2 |

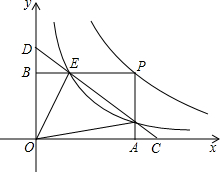 如图,点P是反比例函数y=
如图,点P是反比例函数y=