题目内容
 已知,如图,在平面直角坐标系内,点A的坐标为(0,12),经过原点的直线l,与经过点A的直线12相交于点B,点B的坐标为(9,3).
已知,如图,在平面直角坐标系内,点A的坐标为(0,12),经过原点的直线l,与经过点A的直线12相交于点B,点B的坐标为(9,3).(1)求直线l1,l2的表达式;
(2)点C为直线l1上一动点,作CD∥y轴交直线l2于点D,若CD=8,求点C的坐标.
考点:两条直线相交或平行问题
专题:计算题
分析:(1)分别利用待定系数法求直线l1,l2的表达式;
(2)根据一次函数图象上点的坐标特征设C(t,
t),由于CD∥y轴,则D点的横坐标也为t,则可得到D点坐标为(t,-t+12),然后利用C、D两点的纵坐标之差的绝对值表示CD的长得到|-t+12-
t|=8,解,再解关于t的绝对值方程求出t的值即可得到C点坐标.
(2)根据一次函数图象上点的坐标特征设C(t,
| 1 |
| 3 |
| 1 |
| 3 |
解答: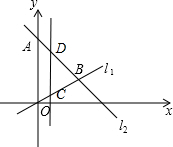 解:(1)设直线l1的解析式为y=ax,
解:(1)设直线l1的解析式为y=ax,
把B(9,3)代入得9a=3,解得a=
,
所以直线l1的解析式为y=
x;
设直线l2的解析式为y=kx+b,
把A(0,12),B(9,3)分别代入得
,解得
,
所以直线l2的解析式为y=-x+12;
(2)设C(t,
t),
因为CD∥y轴,
所以D点坐标为(t,-t+12),
所以|-t+12-
t|=8,解得t=3或t=15,
所以C点坐标为(3,1)或(15,5).
 解:(1)设直线l1的解析式为y=ax,
解:(1)设直线l1的解析式为y=ax,把B(9,3)代入得9a=3,解得a=
| 1 |
| 3 |
所以直线l1的解析式为y=
| 1 |
| 3 |
设直线l2的解析式为y=kx+b,
把A(0,12),B(9,3)分别代入得
|
|
所以直线l2的解析式为y=-x+12;
(2)设C(t,
| 1 |
| 3 |
因为CD∥y轴,
所以D点坐标为(t,-t+12),
所以|-t+12-
| 1 |
| 3 |
所以C点坐标为(3,1)或(15,5).
点评:本题考查了两条直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.会利用待定系数法求一次函数解析式.

练习册系列答案
相关题目
 如图,在?ABCD中,AB=3,AD=4,E是CD的中点,则EO等于( )
如图,在?ABCD中,AB=3,AD=4,E是CD的中点,则EO等于( )| A、3 | B、4 | C、1.5 | D、2 |
下列运动属于平移的是( )
| A、冷水加热过程中小气泡上升成大气泡 |
| B、打开教室门,门的移动 |
| C、上升的电梯 |
| D、随风飘动的风筝在空中运动 |
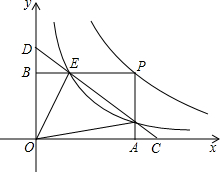 如图,点P是反比例函数y=
如图,点P是反比例函数y= 如图,⊙O是△ABC的内切圆,点D、E分别为边AC、BC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是( )
如图,⊙O是△ABC的内切圆,点D、E分别为边AC、BC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是( )
 某机械传动装置在静止时如图,连杆PB与点B运动所形成的⊙O交于点A,测得PA=4cm,AB=6cm,⊙O半径为5cm,求点P到圆心O的距离.
某机械传动装置在静止时如图,连杆PB与点B运动所形成的⊙O交于点A,测得PA=4cm,AB=6cm,⊙O半径为5cm,求点P到圆心O的距离. 如图,△ABC的三条角平分线交于点P,已知∠ABC=60°,则∠APC=
如图,△ABC的三条角平分线交于点P,已知∠ABC=60°,则∠APC=