题目内容
20. 在平面直角坐标系xOy中,给出如下定义:对于点P(m,n),若点Q(2-m,n-1),则称点Q为点P的“δ点”.例如:点(-2,5)的“δ点”坐标为(4,4).
在平面直角坐标系xOy中,给出如下定义:对于点P(m,n),若点Q(2-m,n-1),则称点Q为点P的“δ点”.例如:点(-2,5)的“δ点”坐标为(4,4).(1)某点的“δ点”的坐标是(-1,3),则这个点的坐标为(3,4);
(2)若点A的坐标是(2-m,n-1),点A的“δ点”为A1点,点A1的“δ点”为A2点,点A2的“δ点”为A3点,…,点A1的坐标是(m,n-2);点A2015的坐标是(4-m),n-2016);
(3)函数y=-x2+2x(x≤1)的图象为G,图象G上所有点的“δ点”构成图象H,图象G与图象H的组合图形记为“图形Ю”,当点(p,q)在“图形Ю”上移动时,若k≤p≤1+2$\sqrt{2}$,-8≤q≤1,则k的取值范围是-2≤k≤1.
分析 (1)设这个点坐标为(m,n),根据“δ点”的定义,列出方程即可解决问题.
(2)从特殊到一般,先探究规律,利用规律即可解决问题.
(3)画出图象,图象G的解析式为y=-x2+2x,(x≤1),图象H的解析式为y=-(x-1)2,(x≥1),对于函数y=-x2+2x,当y=-8时,-x2+2x=-8,解得x=-2或8(舍弃),当y=1时,-x2+2x=1,解得x=1,观察图象,即可解决问题.
解答 解:(1)设这个点坐标为(m,n),
∵这个点的“δ点”的坐标是(-1,3),
∴2-m=-1,n-1=3,
∴m=3,n=4,
∴这个点的坐标为(3,4),
故答案为(3,4).
(2)由题意A1(m,n-2),A2(m-2,n-3),A3(4-m,n-4),A4(m-2,n-5),A5(4-m,n-6),…
由此规律可知A2015(4-m,n-2016).
故答案分别为(m,n-2),(4-m,n-2016).
(3)如图,由题意图象G的解析式为y=-x2+2x,(x≤1),图象H的解析式为y=-(x-1)2,(x≥1)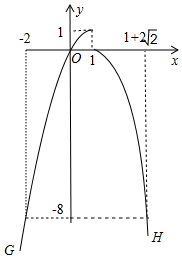
对于函数y=-x2+2x,当y=-8时,-x2+2x=-8,
解得x=-2或8(舍弃),
∴x=-2,
当y=1时,-x2+2x=1,解得x=1,
∵当点(p,q)在“图形Ю”上移动时,若k≤p≤1+2$\sqrt{2}$,-8≤q≤1,
∴由图象可知,-2≤k≤1.
故答案为-2≤k≤1.
点评 本题考查二次函数综合题、解题的关键是理解题意,学会从特殊到一般探究规律,利用规律解决问题,学会利用图象解决问题,属于中考压轴题.

练习册系列答案
相关题目
11. 如图,△AOB和△ACD均为正三角形,且顶点B、D均在反比例函数y=$\frac{4}{x}$在第一象限的图象上,BC、AD交于P,则△OBP的面积是( )
如图,△AOB和△ACD均为正三角形,且顶点B、D均在反比例函数y=$\frac{4}{x}$在第一象限的图象上,BC、AD交于P,则△OBP的面积是( )
 如图,△AOB和△ACD均为正三角形,且顶点B、D均在反比例函数y=$\frac{4}{x}$在第一象限的图象上,BC、AD交于P,则△OBP的面积是( )
如图,△AOB和△ACD均为正三角形,且顶点B、D均在反比例函数y=$\frac{4}{x}$在第一象限的图象上,BC、AD交于P,则△OBP的面积是( )| A. | 4 | B. | 4$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
15.已知x2-(2x+8)=0,则3x2-6(x+3)的值为( )
| A. | 54 | B. | 6 | C. | -10 | D. | -18 |
5.下列命题中,真命题是( )
| A. | 两对角线相等的四边形是矩形 | |
| B. | 两对角线互相平分的四边形是平行四边形 | |
| C. | 两对角线互相垂直的四边形是菱形 | |
| D. | 两对角线互相垂直且平分的四边形是正方形 |
10.下列说法正确的是( )
| A. | “a是任意实数,则a2≥0”是随机事件 | |
| B. | 某彩票的中奖率为1%,则买100张彩票一定有1张会中奖 | |
| C. | 若某运动员投篮2次,投中1次,则该运动员投1次篮,投中的概率为$\frac{1}{2}$ | |
| D. | 口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球 |
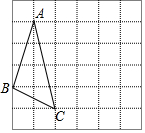 如图网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,建立适当的坐标系,使得B、C两点的坐标分别为B(-1,-1),C(1,-2),将△ABC绕点C顺时针旋转90°,得到△A′B′C′.
如图网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,建立适当的坐标系,使得B、C两点的坐标分别为B(-1,-1),C(1,-2),将△ABC绕点C顺时针旋转90°,得到△A′B′C′.