题目内容
如图,
(1)在图1中,猜想:∠A1+∠B1+∠C1+∠A2+∠B2+∠C2= 度.并试说明你猜想的理由.
(2)如果把图1称为2环三角形,它的内角和为:∠A1+∠B1+∠C1+∠A2+∠B2+∠C2;
图2称为2环四边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠A2+∠B2+∠C2+∠D2;
图3称为2环5五边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠E1++∠A2+∠B2+∠C2+∠D2+∠E2
请你猜一猜,2环n边形的内角和为 度(只要求直接写出结论).
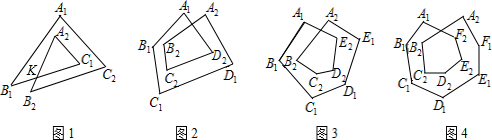
(1)在图1中,猜想:∠A1+∠B1+∠C1+∠A2+∠B2+∠C2=
(2)如果把图1称为2环三角形,它的内角和为:∠A1+∠B1+∠C1+∠A2+∠B2+∠C2;
图2称为2环四边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠A2+∠B2+∠C2+∠D2;
图3称为2环5五边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠E1++∠A2+∠B2+∠C2+∠D2+∠E2
请你猜一猜,2环n边形的内角和为

考点:多边形内角与外角,三角形内角和定理
专题:规律型
分析:(1)连结B1B2,可得∠A2+∠C1=∠B1B2A2+∠B2B1C1,再根据四边形的内角和公式即可求解;
(2)A1A2之间添加两条边,可得B2+∠C2+∠D2=∠EA1D+∠A1EA2+∠EA2B2,再根据边形的内角和公式即可求解;2环n边形添加(n-2)条边,再根据边形的内角和公式即可求解.
(2)A1A2之间添加两条边,可得B2+∠C2+∠D2=∠EA1D+∠A1EA2+∠EA2B2,再根据边形的内角和公式即可求解;2环n边形添加(n-2)条边,再根据边形的内角和公式即可求解.
解答:解:(1)连结B1B2,

则∠A2+∠C1=∠B1B2A2+∠B2B1C1,
∠A1+∠B1+∠C1+∠A2+∠B2+∠C2=∠A1+∠B1+∠B1B2A2+∠B2B1C1+∠B2+∠C2=360度;
(2)如图,A1A2之间添加两条边,
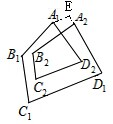
可得B2+∠C2+∠D2=∠EA1D+∠A1EA2+∠EA2B2
则∠A1+∠B1+∠C1+∠D1+∠A2+∠B2+∠C2+∠D2=∠A1+∠B1+∠C1+∠D1+∠A2+∠EA1D+∠A1EA2+∠EA2B2=720°;
2环n边形添加(n-2)条边,2环n边形的内角和成为(2n-2)边形的内角和.其内角和为180(2n-4)=360(n-2)度.
故答案为:(1)360;(2)360(n-2)

则∠A2+∠C1=∠B1B2A2+∠B2B1C1,
∠A1+∠B1+∠C1+∠A2+∠B2+∠C2=∠A1+∠B1+∠B1B2A2+∠B2B1C1+∠B2+∠C2=360度;
(2)如图,A1A2之间添加两条边,

可得B2+∠C2+∠D2=∠EA1D+∠A1EA2+∠EA2B2
则∠A1+∠B1+∠C1+∠D1+∠A2+∠B2+∠C2+∠D2=∠A1+∠B1+∠C1+∠D1+∠A2+∠EA1D+∠A1EA2+∠EA2B2=720°;
2环n边形添加(n-2)条边,2环n边形的内角和成为(2n-2)边形的内角和.其内角和为180(2n-4)=360(n-2)度.
故答案为:(1)360;(2)360(n-2)
点评:考查了多边形内角和定理:(n-2)•180° (n≥3)且n为整数).

练习册系列答案
相关题目
下列图形中,既是轴对称图形,又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 已知:如图,△ABC中,以AB为直径的⊙O交BC于点P,且P为BC中点,PD⊥AC于点D.
已知:如图,△ABC中,以AB为直径的⊙O交BC于点P,且P为BC中点,PD⊥AC于点D. 如图,已知点A(3,2)和点E是正比例函数y=ax与反比例函数
如图,已知点A(3,2)和点E是正比例函数y=ax与反比例函数
 如图,D为△ABC边BC延长线上一点,且CD=CA,E是AD的中点,CF平分∠ACB交AB于点F.求证:CE⊥CF.
如图,D为△ABC边BC延长线上一点,且CD=CA,E是AD的中点,CF平分∠ACB交AB于点F.求证:CE⊥CF.