题目内容
在△ABC中,AB<AC,AD是BC边上的高,AE是角平分线,
(1)若∠B=45°,∠C=35°,则∠DAE= ;
(2)若∠B=70°,∠C=40°,则∠DAE= ;
(3)由(1)、(2)你能猜想出∠DAE与∠B、∠C之间的关系为 .
(1)若∠B=45°,∠C=35°,则∠DAE=
(2)若∠B=70°,∠C=40°,则∠DAE=
(3)由(1)、(2)你能猜想出∠DAE与∠B、∠C之间的关系为
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)根据三角形的内角和定理和∠B=45°,∠C=35°,得出∠BAC=100°,再根据AE是∠BAC角平分线,得出∠BAD=∠DAC=50°,
再根据AD是BC边上的高,求出∠BAD=45°,从而得出答案;
(2)由三角形的内角和定理,可求∠BAC=70°,又由AE是∠BAC的平分线,可求∠BAE=35°,再由AD是BC边上的高,可知∠ADB=90°,可求∠BAD=20°,
从而得出答案;
(3)根据(1)(2)得出的数据即可得出∠DAE与∠B、∠C之间的关系为∠DAE=
(∠B-∠C).
再根据AD是BC边上的高,求出∠BAD=45°,从而得出答案;
(2)由三角形的内角和定理,可求∠BAC=70°,又由AE是∠BAC的平分线,可求∠BAE=35°,再由AD是BC边上的高,可知∠ADB=90°,可求∠BAD=20°,
从而得出答案;
(3)根据(1)(2)得出的数据即可得出∠DAE与∠B、∠C之间的关系为∠DAE=
| 1 |
| 2 |
解答: 解:(1)根据题意如图:
解:(1)根据题意如图:
∵∠B=45°,∠C=35°,
∴∠BAC=100°,
∵AE是∠BAC角平分线,
∴∠BAD=∠DAC=50°,
∵AD是BC边上的高,
∴∠BAD=180°-∠B-∠BDA=45°,
∴∠DAE=∠BAE-∠BAD=50°-45°=5°;
故答案为:5°;
(2)∵∠BAC=180°-∠B-∠C=70°,
∵AE是∠BAC的平分线,
∴∠BAE=∠CAE=35°.
∵AD是BC边上的高,
∴∠ADB=90°,
∵在△ABD中∠BAD=90°-∠B=20°,
∴∠DAE=∠BAE-∠BAD=15°.
故答案为:10°;
(3)由(1)、(2)你能猜想出∠DAE与∠B、∠C之间的关系为:
∠DAE=
(∠B-∠C).
 解:(1)根据题意如图:
解:(1)根据题意如图:∵∠B=45°,∠C=35°,
∴∠BAC=100°,
∵AE是∠BAC角平分线,
∴∠BAD=∠DAC=50°,
∵AD是BC边上的高,
∴∠BAD=180°-∠B-∠BDA=45°,
∴∠DAE=∠BAE-∠BAD=50°-45°=5°;
故答案为:5°;
(2)∵∠BAC=180°-∠B-∠C=70°,
∵AE是∠BAC的平分线,
∴∠BAE=∠CAE=35°.
∵AD是BC边上的高,
∴∠ADB=90°,
∵在△ABD中∠BAD=90°-∠B=20°,
∴∠DAE=∠BAE-∠BAD=15°.
故答案为:10°;
(3)由(1)、(2)你能猜想出∠DAE与∠B、∠C之间的关系为:
∠DAE=
| 1 |
| 2 |
点评:本题考查三角形的内角和定理及角平分线的性质,高线的性质,解答的关键是三角形的内角和定理,一定要熟稔于心.

练习册系列答案
相关题目
已知方程:x3-3x2+(m+2)x-m=0的三个互不相等的实数根为一个三角形三边的长,则实数m的取值范围是( )
| A、0<m<1 | ||
B、m>
| ||
C、
| ||
D、1<m<
|
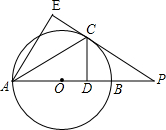 如图,⊙O中,AB是直径,AC是弦,CD⊥AB于D,将△ACD沿AC折叠得到△ACE,延长EC交AB的延长线于点P.
如图,⊙O中,AB是直径,AC是弦,CD⊥AB于D,将△ACD沿AC折叠得到△ACE,延长EC交AB的延长线于点P.