Question

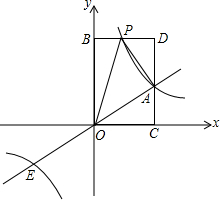如图，已知点A（3，2）和点E是正比例函数y=ax与反比例函数y=

k

x

的图象的两个交点．
（1）填空：点E坐标：

 

；不等式ax＞

k

x

的解集为

 

；
（2）求正比例函数和反比例函数的关系式；
（3）P（m，n）是函数y=

k

x

图象上的一个动点，其中0＜m＜3．过点P作PB⊥y轴于点B，过点A作AC⊥x轴于点C，直线PB、AC交于点D．当P为线段BD的中点时，求△POA的面积．

Answer 1

考点：反比例函数与一次函数的交点问题

专题：

分析：（1）点E的坐标是点A关于坐标原点的中心对称点，所以点E（-3，-2），观察图象即可求得不等式ax＞

k

x

的解集．
（2）把A的坐标代入解析式求出a、k即可；
（3）P为线段BD的中点求出P点的坐标值，然后用矩形的面积减去三个三角形的面积即可．

解答：解：（1）点E坐标：（-3，-2），
不等式ax＞

k

x

的解集为：x＞3或-3＜x＜0．

（2）把A（3，2）代入y=ax
得：2=3a，
解得：a=

2

3

，
∴y=

2

3

x，
代入y=

k

x

得：k=6，
∴y=

6

x

，
∴正比例函数与反比例函数的解析式分别是y=

2

3

x，y=

6

x

．

（3）∵P为线段BD的中点，BD=OC=3，
∴P点的横坐标为

3

2

，
代入y=

6

x

，
得y=4，
∴P（

3

2

，4）；
S_△AOP=S_矩形OCDB-S_△AOC-S_△BOP-S_△APD=3×4-

1

2

×2×3-

1

2

×

3

2

×4-

1

2

×

3

2

×2=

9

2

．

点评：本题主要考查对用待定系数法求出正比例函数、反比例函数的解析式，反比例函数图象上点的坐标特征，三角形的面积等知识点的理解和掌握，能综合运用性质进行计算是解此题的关键．