题目内容
1.计算与化简:(1)(-2)+(-3)-(+1)-(-6)
(2)-22×$\frac{1}{2}$-(-1$\frac{3}{5}$)2$÷(-\frac{4}{5})$-(-1)5
(3)x+[-x-2(x-2y)]
(4)2(x-3)-3(x-5)=7(x-1)
(5)$\frac{x}{2}-\frac{5x+12}{6}$=1+$\frac{2x-4}{3}$.
分析 (1)原式利用减法法则变形,计算即可得到结果;
(2)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(3)原式去括号合并即可得到结果;
(4)方程去括号,移项合并,把x系数化为1,即可求出解;
(5)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)原式=-2-3-1+6=-6+6=0;
(2)原式=-2+$\frac{64}{25}$×$\frac{5}{4}$+1=-1+$\frac{16}{5}$=$\frac{11}{5}$;
(3)原式=x-x-2x+4y=-2x+4y;
(4)去括号得:2x-6-3x+15=7x-7,
移项合并得:8x=16,
解得:x=2;
(5)去分母得:3x-(5x+12)=6+2(2x-4),
去括号得:3x-5x-12=6+4x-8,
移项合并得:6x=-10,
解得:x=-$\frac{5}{3}$.
点评 此题考查了有理数的混合运算,以及解一元一次方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
12. 如图,已知△ABC≌△EDF,下列结论正确的是( )
如图,已知△ABC≌△EDF,下列结论正确的是( )
 如图,已知△ABC≌△EDF,下列结论正确的是( )
如图,已知△ABC≌△EDF,下列结论正确的是( )| A. | ∠A=∠E | B. | ∠B=∠DFE | C. | AC=ED | D. | BF=DF |
9.在△ABC和△DEF中,给出下列四组条件:
①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;
③∠B=∠E,BC=EF,AC=DF;④∠A=∠D,∠B=∠E,∠C=∠F.
其中,能使△ABC≌△DEF的条件共有( )
①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;
③∠B=∠E,BC=EF,AC=DF;④∠A=∠D,∠B=∠E,∠C=∠F.
其中,能使△ABC≌△DEF的条件共有( )
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离为( )
如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离为( )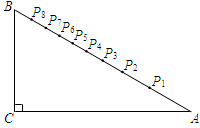 如图,小明设计了一个“简易量角器”:在△ABC中,∠C=90°,∠A=30°,CA=24cm,在AB边上有一系列点P1,P2,P3…P8,使得∠P1CA=10°,∠P2CA=20°,∠P3CA=30°,…∠P8CA=80°.
如图,小明设计了一个“简易量角器”:在△ABC中,∠C=90°,∠A=30°,CA=24cm,在AB边上有一系列点P1,P2,P3…P8,使得∠P1CA=10°,∠P2CA=20°,∠P3CA=30°,…∠P8CA=80°.