题目内容
11.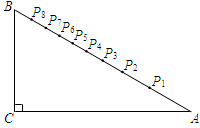 如图,小明设计了一个“简易量角器”:在△ABC中,∠C=90°,∠A=30°,CA=24cm,在AB边上有一系列点P1,P2,P3…P8,使得∠P1CA=10°,∠P2CA=20°,∠P3CA=30°,…∠P8CA=80°.
如图,小明设计了一个“简易量角器”:在△ABC中,∠C=90°,∠A=30°,CA=24cm,在AB边上有一系列点P1,P2,P3…P8,使得∠P1CA=10°,∠P2CA=20°,∠P3CA=30°,…∠P8CA=80°.(1)连接P6C,求∠AP6C的度数;
(2)求线段P6P2的长(结果精确到1cm,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).
分析 (1)根据题意先作出合适的辅助线,然后根据题意可以求得∠AP6C的度数;
(2)根据在△ABC中,∠C=90°,∠A=30°,CA=24cm,可以求得P6C的长度,然后根据第一问求得的∠AP6C的度数,可以求得线段P6P2的长.
解答 解:(1)如下图一所示: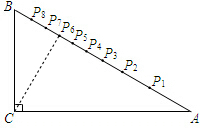
∵在AB边上有一系列点P1,P2,P3…P8,使得∠P1CA=10°,∠P2CA=20°,∠P3CA=30°,…∠P8CA=80°,
∴∠P6CA=60°,
∵∠A=30°,
∴∠AP6C=180°-∠P6CA-∠A=180°-60°-30°=90°,
即∠AP6C的度数是90°;
(2)∵在△ABC中,∠C=90°,∠A=30°,CA=24cm,∠AP6C=90°,
∴AC=2P6C,
∴P6C=12cm,
∵∠P2CA=20°,∠A=30°,
∴∠CP2P6=∠P2CA+∠A=50°,
∵$tan∠C{P}_{2}{P}_{6}=\frac{C{P}_{6}}{{P}_{6}{P}_{2}}$,tan50°≈1.20,
∴${P}_{6}{P}_{2}=\frac{C{P}_{6}}{tan∠C{P}_{2}{P}_{6}}=\frac{12}{1.20}=10$cm,
即线段P6P2的长是10cm.
点评 本题考查解直角三角形的应用,解题的关键是明确题意,找出各边之间的关系,然后找出所求问题需要的条件.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
2.方程组$\left\{\begin{array}{l}{x-y=2}\\{2x+y=1}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ |