题目内容
15.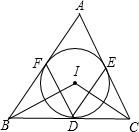 已知⊙I为△ABC的内切圆,点D,E,F是切点,连接BI,CI,DE,DF,试猜想∠BIC与∠FDE有何数量关系,并证明你的猜想.
已知⊙I为△ABC的内切圆,点D,E,F是切点,连接BI,CI,DE,DF,试猜想∠BIC与∠FDE有何数量关系,并证明你的猜想.
分析 根据圆I是△ABC的内切圆求出∠IBC+∠ICB=$\frac{1}{2}$(∠ABC+∠ACB),根据三角形的内角和求得∠BIC=180°-(∠IBC+∠ICB)=180°-$\frac{1}{2}$(∠ABC+∠ACB)=90°+$\frac{1}{2}∠$A,连接IF、IE,求出∠FIE,即可求出∠EDF=$\frac{1}{2}$∠EIF=90°-$\frac{1}{2}∠$A,即可求出答案.
解答 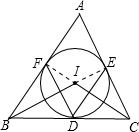 解:∵圆I是△ABC的内切圆,
解:∵圆I是△ABC的内切圆,
∴∠IBC=$\frac{1}{2}$∠ABC,∠ICB=$\frac{1}{2}$∠ACB,
∴∠IBC+∠ICB=$\frac{1}{2}$(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°-∠A
∴∠BIC=180°-(∠IBC+∠ICB)=180°-$\frac{1}{2}$(∠ABC+∠ACB)=90°+$\frac{1}{2}∠$A,
连接IF、IE,
∵圆I是△ABC的内切圆,
∴∠IFA=∠IEA=90°,
∴∠FIE=360°-∠IFA-∠IEA-∠A=180°-∠A,
∴∠EDF=$\frac{1}{2}$∠EIF=90°-$\frac{1}{2}∠$A,
∴∠BIC+∠FDE=90°+$\frac{1}{2}∠$A+90°-$\frac{1}{2}∠$A=180°.
点评 本题主要考查对三角形的内角和定理,三角形的内切圆与内心,圆周角定理等知识点的理解和掌握,能熟练地运用性质进行推理是解此题的关键.

练习册系列答案
相关题目
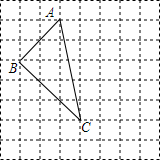 在如图所示的正方形网格中,格点三角形ABC(即顶点都是网格线的交点)的顶点A、C的坐标为A(-1,4)、B(-3,2).
在如图所示的正方形网格中,格点三角形ABC(即顶点都是网格线的交点)的顶点A、C的坐标为A(-1,4)、B(-3,2).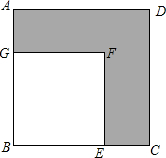 如图,工人张师傅要在一块大正方形ABCD中切下一块小的正方形BEFG,若阴影部分面积为240mm2,AB=2x+8,BE=2x-4,求大正方形的边长.
如图,工人张师傅要在一块大正方形ABCD中切下一块小的正方形BEFG,若阴影部分面积为240mm2,AB=2x+8,BE=2x-4,求大正方形的边长.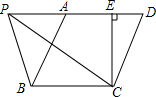 如图,?ABCD中,BC=5cm,CD=6cm,CE⊥AD于点E,CE=4cm,P为直线AD上一点.求;
如图,?ABCD中,BC=5cm,CD=6cm,CE⊥AD于点E,CE=4cm,P为直线AD上一点.求;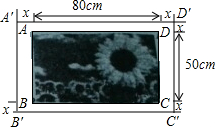 如图,在一幅长为80cm,宽为50cm的矩形画ABCD的四周镶一条金色纸边,制成一幅矩形挂图A′B′C′D′.如果金色镶边纸的宽度x为5cm,那么原风景画ABCD与矩形挂图A′B′C′D′是否相似?并说明理由.
如图,在一幅长为80cm,宽为50cm的矩形画ABCD的四周镶一条金色纸边,制成一幅矩形挂图A′B′C′D′.如果金色镶边纸的宽度x为5cm,那么原风景画ABCD与矩形挂图A′B′C′D′是否相似?并说明理由.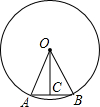 如图,⊙O的半径为20,$\widehat{AB}$的度数为36°,求弦AB及其弦心距OC的长(精确到0.1).
如图,⊙O的半径为20,$\widehat{AB}$的度数为36°,求弦AB及其弦心距OC的长(精确到0.1).